环路与面公式

定义

散度

单位体积的通量

旋度

单位面积的环量

静电场

Stokes 公式

$\displaystyle\oint_{L} f \cdot dL= \iint_{S} (\nabla \times f)\cdot dS$

电场环路定律

$\displaystyle\int E\cdot dl=0$

通过 Stokes 公式, 电场环路定律推出微分形式

$\displaystyle\int E\cdot dl= \iint(\nabla\times E)dA$

在静电场中有环路定律：

$\displaystyle\int E\cdot dl=0$

$\displaystyle\therefore \nabla\times E = 0$

事实上，在 Faraday 电磁感应定律中，磁通量变化时：

$\displaystyle\int E\cdot dl= -\frac {d\Phi} {dt}=\epsilon (电势差)$

$\displaystyle \Phi=\oiint B\cdot dA$

$\displaystyle \therefore \oint E\cdot dl= -\oiint \frac{\partial B}{\partial t}\cdot dA$

$\displaystyle\therefore \nabla\times E = -\frac{\partial B}{\partial t}$

Gauss 公式

$\displaystyle\oiint_{S} f\cdot dS= \iiint_{V} (\nabla\cdot f )\cdot dV$

Gauss 电场定理

$\displaystyle\oiint_{S} E\cdot dS =\frac{\sum_{inside} q}{\epsilon_0}$

通过 Gauss 公式, Gauss 电场定理推出 Gauss 电场定律微分形式

$\displaystyle\oiint_{S} E\cdot dS =\frac{q}{\epsilon_0} =\iiint_{V} \frac{\rho}{\epsilon_0}dV=\iiint_{V} (\nabla\cdot E)dV$

$\displaystyle \therefore \nabla\cdot E = \frac{\rho}{\epsilon_0}$

恒磁场

Ampere 磁场环路定律

$\displaystyle\int B\cdot dl=\mu_0 \sum_{inside} i$

$\sum_{inside} i$ 指被环路包围的电流

Gauss 磁场定理

$\displaystyle\oiint_{S} B\cdot dS =0$

同样用两个数学公式推导出微分形式

$\nabla \cdot B = 0$

$\nabla \times B = \mu_0 j$

电偶极矩/磁偶极矩

电偶极矩

$p = ql$

$\tau = p\times E$

$U = -p \cdot E$

极化强度矢量 $P=\frac{\sum p_m}V$

$\oiint P\cdot dA = -\sum_{in}q'$

$q'$ 是束缚电荷 (induced charge)

一般求电荷默认用 $E$, 指明是 束缚电荷 再用 $P$

球坐标系: $\rho'=-\nabla\cdot P=-\frac{1}{r^2}\frac{\partial r^2P}{\partial r}$

柱坐标系: $\rho'=-\nabla\cdot P=-\frac{\partial P}{\partial z}$

$P\cdot n = \sigma_e'$ (电荷面密度)

电位移矢量/电感应强度 $D=\epsilon_0 E+P$

$\oiint D\cdot dA = \sum_{in}q_0$

磁偶极矩

$\mu = iA$

$\tau = \mu \times B$

$U = -\mu \cdot B$

磁化强度矢量 $M=\frac{\sum \mu_m}V$

$\oint M\cdot dl = \sum_{in}i'$

$M\times n = j'$ (电流线密度)

注意是线密度!

与麦克斯韦方程组的 $\nabla \times H=j_0$ 的电流密度不同

磁场强度 $H=\frac{B}{\mu_0}-M$

$\oint H\cdot dl = \sum_{in}i_0$

电位移矢量 (电感应强度) 高斯定理

$\displaystyle \because \oiint P\cdot dA = -\sum_{in}q'$

$\epsilon_0\displaystyle \oiint E\cdot dA = \sum_{in}(q'+q_0)$

$\displaystyle \therefore \oiint(\epsilon_0E+P)\cdot dA=q_0$

$\displaystyle \oiint D\cdot dA=q_0$

磁场强度高斯定理

$\displaystyle \because \oint M\cdot dl = \sum_{in}i'$

$\displaystyle \frac1{\mu_0}\oint B\cdot dl = \sum_{in}(i'+i_0)$

$\displaystyle \therefore \oint(\frac B{\mu_0}-M)\cdot dl=i_0$

$\displaystyle \oint H\cdot dl=i_0$

电场强度	电感应强度	磁感应强度	磁场强度
$E$	$D=\epsilon_0 E+P$	$B$	$H=\frac{B}{\mu_0}-M$

$D=\kappa_e \epsilon_0 E$

$B=\kappa_m \mu_0 H$

介电常数

$\kappa_e\geq 1$

例: 圆柱形区域内, $P=P_0z/L$, 那么得到 $\rho'=-\nabla \cdot P = -\frac{\partial P}{\partial z}=-P_0/L$, 因此高斯定理得到$E=-P_0z/L$, 说明 $D=0$ 且 $E\not =0$, 那么 $\kappa_e=0$

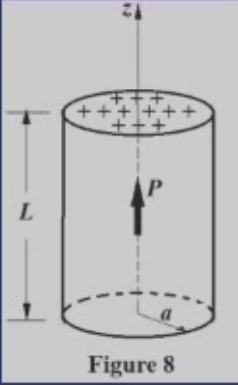
alt text

问题出在 $D=\kappa_e \epsilon_0 E$ 这个公式只适用于各向同性的线性电介质

这句话有点抽象, 但这题的电介质大概就不满足这个条件

所以我们不能只通过 $D=0$ 来说 $\kappa_e=0$

介质中的电场

有 $\displaystyle E=\frac{E_0}{\kappa_e}$

电流密度

单位面积电流:

$\displaystyle j=\sigma E$

$\displaystyle i=\iint_A j\cdot dA$

电源内部:

$\displaystyle \overset{\rightarrow}j=\sigma (\overset{\rightarrow}K+\overset{\rightarrow}E)$

$\displaystyle \overset{\rightarrow}K$ 是非静电力, 把电荷从负极搬运到正极

能量密度

单位体积能量:

$\displaystyle u=\frac12\frac{B^2}{\mu_0}=\frac12B\cdot H$

$\displaystyle u=\frac12\epsilon_0E^2=\frac12D\cdot E$

注意这个式子太微观了, 不能直接用在点电荷上

能量

弹性势能

$\displaystyle E=\frac12kx^2$

动能

$\displaystyle E=\frac12mv^2$

电容能量

$\displaystyle E=\frac12\frac{Q^2}{C}=\frac12CU^2=\frac12QU$

电感能量

$\displaystyle U=\frac12LI^2$

$\displaystyle U=\frac12\sum_{i}L_iI_i^2+\frac12\sum_{i,j}M_{ij}I_iI_j$

电场能量

$\displaystyle U=\iiint u_E dV$

磁场能量

$\displaystyle U=\iiint u_B dV$

球坐标下的算子

梯度

$\displaystyle \nabla T= \dfrac{\partial T}{\partial r}\hat{r}+\dfrac{1}{r}\dfrac{\partial T}{\partial\theta}\hat{\theta}+\dfrac{1}{\sin \theta \cdot r}\dfrac{\partial T}{\partial \phi}\hat{\phi}$

暴力推导

散度

$ \displaystyle \nabla\cdot T = \frac{1}{r^2} \frac{\partial}{\partial{r}} (r^2 T_r) + \frac{1}{r\sin \theta} \frac{\partial}{\partial{\theta}} (\sin\theta T_\theta) + \frac{1}{r\sin \theta} \frac{\partial T_\phi}{\partial \phi} $

旋度

$ \displaystyle\nabla\times T = \frac{1}{r\sin \theta} \left[ \frac{\partial}{\partial{\theta}} (\sin \theta T_\phi) - \frac{\partial}{\partial{\phi}} \right] \hat{\boldsymbol{\mathbf{r}}} + \frac1r \left[\frac{1}{\sin \theta} \frac{\partial T_r}{\partial \phi} - \frac{\partial}{\partial{r}} (r T_\phi) \right] \hat{\boldsymbol{\mathbf{\theta}}} + \frac1r \left[ \frac{\partial}{\partial{r}} (r T_\theta) - \frac{\partial T_r}{\partial \theta} \right] \hat{\boldsymbol{\mathbf{\phi}}} $

柱坐标下的算子

梯度

$\displaystyle \nabla T= \dfrac{\partial T}{\partial r}\hat{r}+\dfrac{1}{r}\dfrac{\partial T}{\partial\theta}\hat{\theta}+\dfrac{\partial T}{\partial z}\hat{z}$

散度

$\displaystyle \nabla \cdot T= \frac1r\dfrac{\partial (rT_r)}{\partial r}+\dfrac{1}{r}\dfrac{\partial T_{\theta}}{\partial\theta}+\dfrac{\partial T_z}{\partial z}$

拉梅系数

电学物理量与电荷，距离关系

$\displaystyle F=\frac{qq_0}{4\pi\epsilon_0r^2}$

$\displaystyle E=\frac{q}{4\pi\epsilon_0r^2}$

$\displaystyle U=\frac{qq_0}{4\pi\epsilon_0r}$

$\displaystyle V=\frac{q}{4\pi\epsilon_0r}$

有关符号

$\displaystyle U_b-U_a=-\int_a^b F\cdot dl$

$\displaystyle V_b-V_a=-\int_a^b E\cdot dl$

$\displaystyle E=-\frac{dV}{dl}$

$\displaystyle E=-\nabla \cdot V$

$\displaystyle f=-e(v\times B)$

$\displaystyle \epsilon=-\frac{d\Phi}{dt}=-M\frac{di}{dt}$

电场强度 $E$

点电荷

$\displaystyle E=\frac1{4\pi\epsilon_0}\frac{q}{r^2}$

长直导线

$\displaystyle E=\frac{\lambda}{2\pi \epsilon_0 r}$

长直导线系数比较特殊

比如电场 $E$ 分母系数是 $2$ 不是 $4$

圆环

$\displaystyle E=\frac{qz}{4\pi \epsilon_0(z^2+R^2)^{3/2}}$

圆盘

$\displaystyle E=\frac{2q}{4\pi \epsilon_0R^2}(1-\frac{1}{\sqrt{1+\frac{R^2}{z^2}}})=\frac{\sigma}{2\epsilon_0}(1-\frac{1}{\sqrt{1+\frac{R^2}{z^2}}})$

就是无限大极板后乘一个系数

无限大极板

$\displaystyle E=\frac{\sigma}{2\epsilon_0}$

电偶极矩

从两个点电荷得出

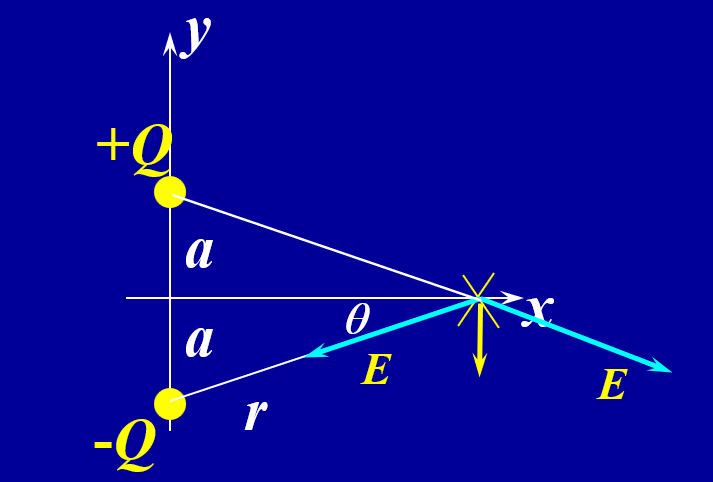
$\displaystyle E_y=\frac1{4\pi\epsilon_0}\frac{2Qa}{(x^2+a^2)^{3/2}}=\frac1{4\pi\epsilon_0}\frac{p}{(x^2+a^2)^{3/2}}=\frac p{4\pi\epsilon_0x^3}[1+(\frac32)(\frac ax)^2+\cdots]=\frac p{4\pi\epsilon_0x^3}$

$p=2Qa$

电势能 $U$

球壳

面均匀分布电荷 $q$, 电势能为 $\displaystyle U=\frac{q^2}{8\pi\epsilon_0R}$

一般求法

$\displaystyle U=\int Vdq$

$q$ 可以是均匀分布在空间/平面的电荷

$V$ 可以是点电荷或其他产生的电势

两两配对

$\displaystyle U=\sum \frac{q_iq_j}{4\pi\epsilon_0r}$

电势 $V$

圆环

$\displaystyle V=\frac{q}{4\pi \epsilon_0\sqrt{z^2+R^2}}$

圆盘

$\displaystyle V=\frac{\sigma}{2\epsilon_0} (\sqrt{z^2+R^2}-z)$

电容 $C$

球壳

空球壳

$\displaystyle C=4\pi\epsilon_0 R$

一般化

$\displaystyle C=4\pi\epsilon_0 \frac{ab}{b-a}$

平行板

$\displaystyle C=\frac{\kappa_e\epsilon_0A}{d}=\frac{\epsilon_0A}{d}$

圆柱体

$\displaystyle C=\frac{2\pi\epsilon_0L}{\ln\frac ba}$

磁感应强度 $B$

电流元

毕奥-萨伐尔：

$\displaystyle B=\frac{\mu_0}{4\pi}\oint_L\frac{ids\times \hat r}{r^2}$

受力为:

$\displaystyle dF=ids\times B$

长直导线

$\displaystyle B=\frac{\mu_0i}{4\pi r}(\cos\theta_1-\cos\theta_2)$

除了这个分母系数是 $4$, 其他都是 $2$

圆环

$\displaystyle B=\frac{\mu_0}{2}\frac{iR^2}{(R^2+z^2)^{3/2}}$

螺线管

$\displaystyle B=\frac12\mu_0ni(\cos\beta_1-\cos\beta_2)$

螺绕环

$\displaystyle B=\frac{\mu_0Ni}{2\pi r}=\mu_0ni$

无限板

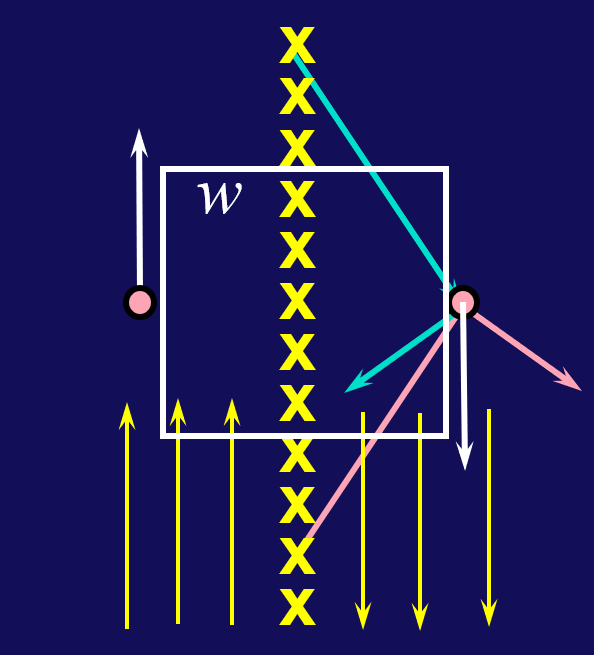
alt text

$\displaystyle B=\frac12 \mu_0ni$

磁偶极矩

从圆环得出

$\displaystyle B=\frac{\mu_0iR^2}{2z^3}=\frac{\mu_0i\pi R^2}{2\pi z^3}=\frac{\mu_0iA}{2\pi z^3}=\frac{\mu_0\mu}{2\pi z^3}$

$\mu=iA$

电感 $L$, 互感 $M$

$\displaystyle M=\frac{\Phi}{i}=\frac{NBA}{i}$

$\displaystyle \epsilon=-\frac{d\Phi}{dt}=-M\frac{di}{dt}$

$\displaystyle \epsilon=-L\frac{di}{dt}$

无限长螺线管

一段 $l$ 对应的自感

$\displaystyle L=\mu_0n^2lA$

长方形螺绕环

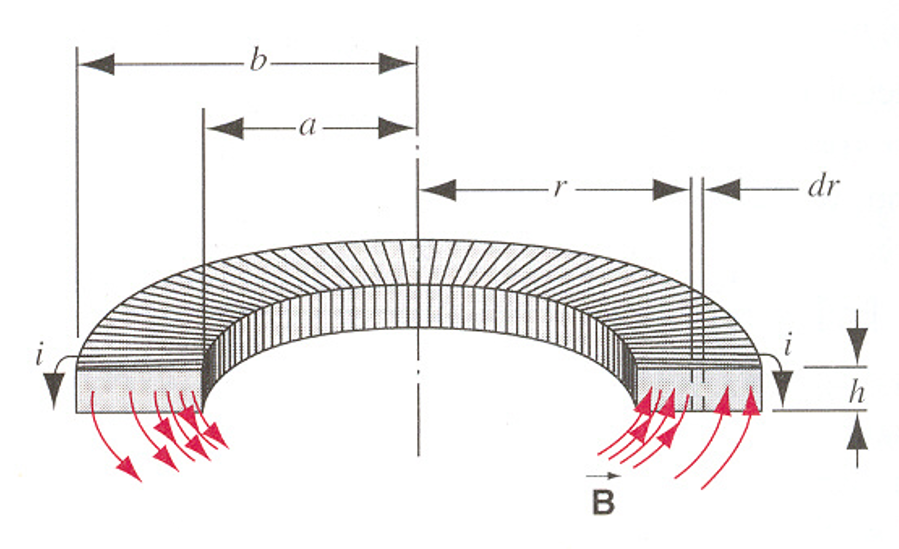
alt text

$\displaystyle L=\frac{\mu_0n^2h}{2\pi}\ln\frac ba$

同轴电缆

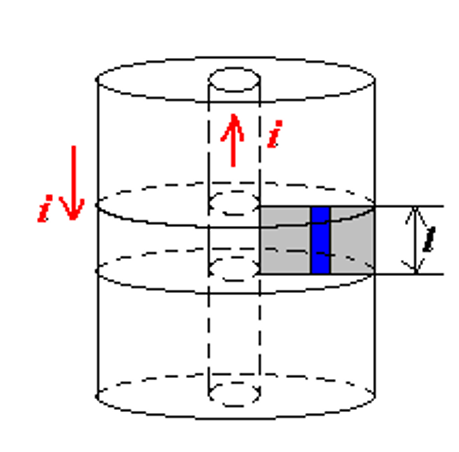
alt text

$\displaystyle L=\frac{\mu_0}{2\pi}l\ln\frac {R_2}{R_1}$

电感与互感

$M=\sqrt{L_1L_2}$

$RC$ 电路

$\displaystyle iR+\frac qC=\epsilon$

$\displaystyle \frac{dq}{dt}+\frac q{CR}=\frac{\epsilon}{R}$

$q=C\epsilon (1-e^{-t/RC})$

$RL$ 电路

通电

$\displaystyle \epsilon +\epsilon_L=iR$

$\displaystyle \epsilon -L\frac{di}{dt}=iR$

$\displaystyle \epsilon =L\frac{di}{dt}+iR$

解微分方程，得到通电时：

$\displaystyle i=\frac{\epsilon}R(1-e^{-Rt/L})$

$\displaystyle V=\epsilon e^{-Rt/L}$ (电压)

放电

$\displaystyle \epsilon_L=iR$

$\displaystyle -L\frac{di}{dt}=iR$

$\displaystyle 0 =L\frac{di}{dt}+iR$

解微分方程，得到放电时：

$\displaystyle i=\frac{\epsilon}Re^{-Rt/L}$

$\displaystyle V=-\epsilon e^{-Rt/L}$

$LC$ 电路

$\displaystyle U=U_L+U_C=\frac 12Li^2+\frac 12\frac {q^2}{C}$

$\displaystyle \frac{dU}{dt}=Li\frac{di}{dt}+\frac{q}{C}\frac{dq}{dt}=0$

$\displaystyle Li\frac{d^2q}{dt^2}+\frac{q}{C}i=0$

$\displaystyle \frac{d^2q}{dt^2}+\frac{1}{LC}q=0$

$\displaystyle \omega = \sqrt{\frac{1}{LC}}$

动生电动势

$\epsilon = \int (v\times B)\cdot dl$

$\epsilon = lv\times B$

$\displaystyle \frac{lv\times B}{R}=\frac{\epsilon}{R}=i=Sj=S\sigma E$

$\displaystyle \therefore \frac{v\times B}{R}\cdot \frac{l}{\sigma S}=\frac{v\times B}{R}\cdot R=v\times B=E$

注意产生的电场是非极化场, $E_0=v\times B$

因为有电动势也有电流, 而电流是自由电荷产生的, 不是束缚电荷

麦克斯韦方程组

修正

到上面为止，有四个方程：

$\left\{\begin{array}{l} \displaystyle \oiint D\cdot dA=q_0 & 高斯电场定理\\ \displaystyle \oiint B\cdot dA=0& 高斯磁场定理\\ \displaystyle \oint E\cdot dl=-\iint\frac{\partial B}{\partial t}\cdot dA& 法拉第感应定律\\ \displaystyle \oint H\cdot dl=i_0=\iint j\cdot dA& 安培环路定律 \end{array}\right.$

但是后两个式子看着不对称

既然有变化的磁场产生电场，也应该有变化的电场产生磁场

所以修正一下：

对于电容器, 如果选择极板中间作为包围电流的面, 那么包围的电流为 $0$

所以在极板间加入真空中的位移电流 $i_D$

$\displaystyle \Phi_D=\iint D\cdot dA$

$\displaystyle i_D=\frac{d\Phi_D}{dt}=\iint \frac{\partial D}{\partial t}\cdot dA$

修改真空中的安培定律: $\displaystyle \oint H\cdot dl=i_0+i_D=\iint(j_0+\frac{\partial D}{\partial t})\cdot dA$

积分形式

真空中：

$\left\{\begin{array}{l} \displaystyle \oiint E\cdot dA=\frac{q}{\epsilon_0}\\ \displaystyle \oiint B\cdot dA=0\\ \displaystyle \oint E\cdot dl=-\iint\frac{\partial B}{\partial t}\cdot dA\\ \displaystyle \oint B\cdot dl=\mu_0i+\mu_0\epsilon_0\iint \frac{\partial E}{\partial t}\cdot dA \end{array}\right.$

介质中：

$\left\{\begin{array}{l} \displaystyle \oiint D\cdot dA=q_0\\ \displaystyle \oiint B\cdot dA=0\\ \displaystyle \oint E\cdot dl=-\iint\frac{\partial B}{\partial t}\cdot dA\\ \displaystyle \oint H\cdot dl=i_0+\iint\frac{\partial D}{\partial t}\cdot dA=\iint (j_0+\frac{\partial D}{\partial t})\cdot dA \end{array}\right.$

微分形式:

真空中：

$\left\{\begin{array}{l} \displaystyle \nabla\cdot E = \frac{\rho}{\epsilon_0}\\ \displaystyle \nabla\cdot B=0\\ \displaystyle \nabla\times E=-\frac{\partial B}{\partial t}\\ \displaystyle \nabla\times B=\mu_0j+\mu_0\epsilon_0 \frac{\partial E}{\partial t} \end{array}\right.$

介质中：

$\left\{\begin{array}{l} \displaystyle \nabla\cdot D = \rho_0\\ \displaystyle \nabla\cdot B=0\\ \displaystyle \nabla\times E=-\frac{\partial B}{\partial t}\\ \displaystyle \nabla\times H=j_0+ \frac{\partial D}{\partial t} \end{array}\right.$

电磁波

电磁波的性质

横波
$\overset{\to}E \bot\overset{\to}H$
$E,H$ 同相位
$\sqrt{\kappa_e\epsilon_0}E_0=\sqrt{\kappa_m\mu_0}H_0$
$\displaystyle v=\frac{1}{\sqrt{\kappa_e\epsilon_0\kappa_m\mu_0}}$

真空中可以由性质 4 推出 $E_0=\frac{B_0}{c}$

1. 横波

波源为圆心取一个球面, 任意一点 $E,H$ 相等

取一个小的近似平面, 为 $x,y$ 平面, 由于任意一点 $E,H$ 相等, 则 $E,H$ 与 $x,y$ 无关

To be continued

波印廷矢量

poynting vector

$S=E\times H$

垂直导线方向为 $i^2R$

平行导线方向为 $i\epsilon$

导线为导体, 所以表面有电荷

所以既有向内生热, 又有向前传给电阻做功

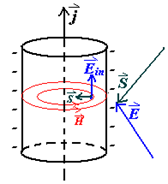
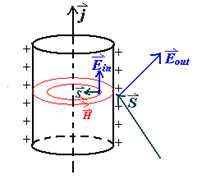
alt text

电源电场为反方向, 所以有向外的 $S$, 这是在向外传递能量, 沿着导线传给电阻

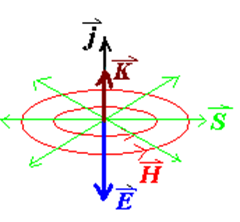
alt text

电阻周围正负电荷抵消, 所以没有能量传递, 只有生热:

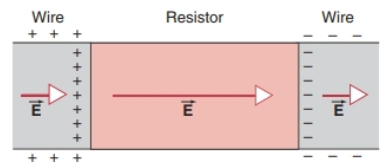
alt text

最后整个图:

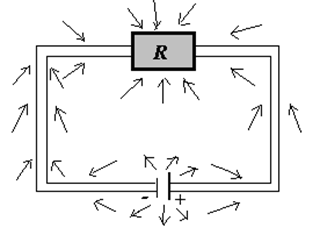
alt text

电阻

$\overset{\to}S$ 向内

$\displaystyle -\oiint \overset{\to}S\cdot dA= \oiint S\cdot dA=i^2R$

电容

$\overset{\to}S$ 向内

$\displaystyle -\oiint \overset{\to}S\cdot dA= \oiint S\cdot dA=\frac{dU}{dt}=Ad\frac{d}{dt}(\frac12 \epsilon_0 E^2)$

电磁波的能量

$\displaystyle \frac{dU}{dt}=-\oiint (E\times H)\cdot dA-\iiint(j_0\cdot E)\cdot dV$

$\displaystyle j_0=\sigma(E+K),E=\rho j_0-K$

$\displaystyle \therefore \iiint(j_0\cdot E)\cdot dV=(j_0\cdot E)\cdot \Delta A\Delta l=\rho j_0^2\Delta A\Delta l - (j_0\Delta A)\cdot (K\Delta l)$

$\displaystyle =\rho\frac{\Delta l}{\Delta A}(j_0\Delta A)^2-(j_0\Delta A)\cdot (K\Delta l)$

$\displaystyle =i_0^2R-i_0\Delta \epsilon$

$\displaystyle \frac{dU}{dt}=-\oiint S\cdot dA-Q+P$

$\displaystyle S=E\times H=\frac{E\times B}{\mu_0}=\frac{EB}{\mu_0}=\frac{E^2}{\mu_0c}=\frac{E^2}{377\Omega}$

强度是最大值的均方根:

$\displaystyle I=\langle S\rangle=\frac12 \frac{E^2}{377\Omega}$

$\displaystyle u=\frac 12\epsilon_0E^2+\frac{B^2}{2\mu_0}=\epsilon_0E^2$

所以 $\displaystyle \langle u\rangle=\frac{\epsilon_0E^2}{2}$

$\displaystyle I=c\langle u\rangle$

同时给出功率 $P$ 与当前位置所在球面 $4\pi r^2$, 则 $I=\frac{P}{4\pi r^2}$

光压

$P=\frac1c (|S_{in}|+|S_{ref}|)$

全部反射: $P=\frac 2c(EH)$

全部吸收: $P=\frac 1c(EH)$

动量密度

$\displaystyle g=\frac{1}{c^2}S=\frac{1}{c^2}(E\times H)$

几何光学

焦距

$\displaystyle \frac{n'}{i}+\frac{n}{o}=\frac{n'-n}{r}$

令 $\displaystyle i\to\infty,o=f=\frac{n}{n'-n}r$

令 $\displaystyle o\to\infty,i=f'=\frac{n'}{n'-n}r$

$\displaystyle \therefore \frac{f'}{f}=\frac{n'}{n},\frac{f'}{i}+\frac{f}{o}=1$

$o=object, i=image$

球面镜成像

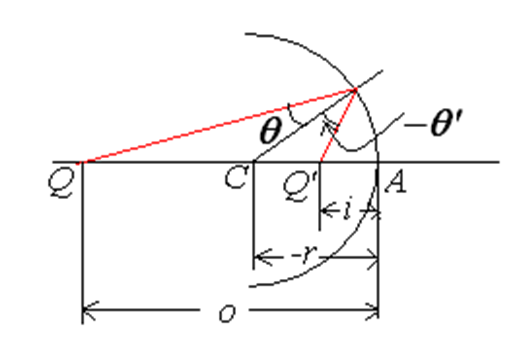
alt text

$n\sin\theta = n'\sin\theta'$

$n=-n'$

$\displaystyle f'=\frac{n'}{n'-n}r=\frac{r}{2}$

$\displaystyle f=\frac{n}{n'-n}r=-\frac{r}{2}$

$\displaystyle \therefore \frac{1}{o}+\frac{1}{i}=-\frac{2}{r}$

磨镜者公式

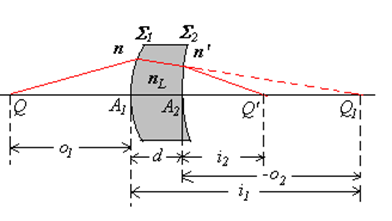
alt text

$\displaystyle f'=\frac{n'}{\frac{n_L-n}{r_1}+\frac{n'-n_L}{r_2}}$

$\displaystyle f=\frac{n}{\frac{n_L-n}{r_1}+\frac{n'-n_L}{r_2}}$

当 $n'=n=1$

$\displaystyle f=f'=\frac{1}{(n_L-1)(\frac1{r_1}-\frac1{r_2})}$

光学的费马定理

叙述

$\displaystyle \delta(PQ) = \delta(\int_P^Q n\cdot dl)=0$

这说明了：

1. 将 $\displaystyle \int_P^Q n\cdot dl$ 看作函数，对其中任意变量求偏导，结果为 $0$

2. $\displaystyle t_{QP}= \frac 1c \int_P^Q n\cdot dl$, 则时间只能取极值或为常值

语言描述就是：光走的路径是用时最短的路径

这也说明第二条性质中，时间取的是极小值

下面给出数学的变分定义，并详细说明这两条性质

数学

泛函

泛函是从函数组成的向量空间到标量域的映射

线性代数里的线性泛函就是从向量空间映射到数域

一般的泛函将函数映射到实数域

例如对于函数做定积分，得到一个实数值，那么这个积分就是对于函数的泛函

变分

微分是变量的变化量，比如自变量从 $x$ 变化到 $x+\Delta x$, 变化量为 $dx=\Delta x$

而变分是指函数的变化量，比如自变量函数从 $y(x)$ 变化到 $y(x) + \Delta y(x)$, 变化量为 $\delta y=\Delta y$，也可写成 $\delta y(x)=\Delta y(x)$

变量的变化量是一个值，函数的变化量是一个函数。所以感性理解一下，微分是针对函数的，变分是针对泛函的

更具体/严格定义变分，应该长成类似这样：

如果函数从 $y(x)$ 变化到 $y(x)+\epsilon \eta(x)$, 那么 $\delta y= \epsilon \eta$, 其中 $\epsilon$ 是一个变量

具体见 wiki

`Euler-Lagrange` 方程

一般的方程为:

$\displaystyle I=\int_a^b F(x, y, y') dx$

如果 $F(x, y, y')=f(y, y')$, 并且 $\frac{\partial F}{\partial x}=0$, 即 $F$ 不显含 $x$

则方程写成:

$\displaystyle I=\int_a^b f(y, y') dx$

$I$ 是函数 $y(x)$ 的一个泛函

我们想要找到一个函数 $y(x)$ 使得 $I$ 取极值

也就是找到 $y(x)$ 使得 $\delta I=0$

事实上，这样的 $y(x)$ 满足 Euler-Lagrange 方程:

$\displaystyle \frac{\partial f}{\partial y}-\frac{d}{dx}\left( \frac{\partial f}{\partial y'}\right)=0$

推导与例子

同时，在 $F$ 不显含 $x$ 时，有等价的式子:

$\displaystyle \frac{d}{dx}(F-y'\frac{\partial F}{\partial y'})=\frac{\partial F}{\partial x}+\frac{dy}{dx}\cdot \frac{\partial F}{\partial y}+\frac{dy'}{dx}\cdot \frac{\partial F}{\partial y'}-\frac{dy'}{dx}\cdot \frac{\partial F}{\partial y'}-y'\frac{d}{dx}(\frac{\partial F}{\partial y'})$

$\displaystyle =\frac{\partial F}{\partial x}+y'[\frac{\partial F}{\partial y}-\frac{d}{dx}(\frac{\partial F}{\partial y'})]=y'[\frac{\partial F}{\partial y}-\frac{d}{dx}(\frac{\partial F}{\partial y'})]$

若 $y'\not=0$, 则 $\displaystyle \frac{\partial F}{\partial y}-\frac{d}{dx}(\frac{\partial F}{\partial y'})=0$ 等价于

\[ F-y'\frac{\partial F}{\partial y'}=c \]

应用到费马定理

费马定理中，$\displaystyle I=\int_P^Qn\cdot dl=\int_{x_1}^{x_2}n(y)\cdot \sqrt{1+y'(x)^2}dx$

$n(y)$ 一般是分段常值函数

$\displaystyle f(y,y')=n(y)\cdot \sqrt{1+y'^2}$, 所以代入上面的式子

$\displaystyle F-y'\frac{\partial F}{\partial y'}=n(y)\cdot \sqrt{1+y'^2}-y'\cdot n(y)\cdot \frac{y'}{\sqrt{1+y'^2}}=\frac{n(y)}{\sqrt{1+y'^2}}=c$

若路径与铅垂线夹角为 $\theta$, 那么 $\displaystyle \cot \theta = \frac{dy}{dx}, \sin \theta = \frac{1}{\sqrt{1+y'^2}}$

首先，对于反射定律:

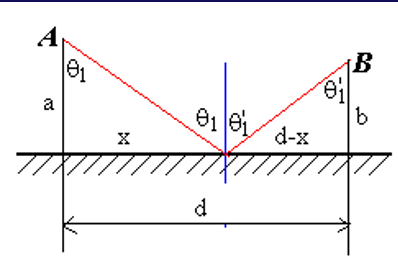
alt text

由于 $n(y)$ 不变，所以 $\sin\theta=\frac{n(y)}{c}$ 不变，所以 $\sin\theta_1=\sin\theta_1'$

其次，对于折射定律:

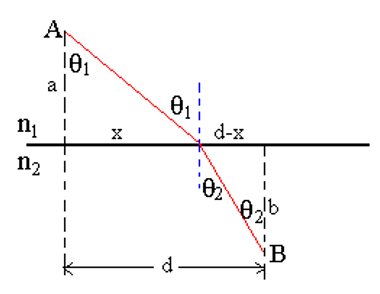
alt text

$n(y)\sin \theta=c$, 即如果 $n$ 是位置的连续函数，则 $n(y)\sin \theta$ 是一个常数

这可以得到折射定律: $n_1\sin\theta_1=n_2\sin\theta_2$

此外还可以得到大气中光线轨迹的微分方程：$\displaystyle \frac{dy}{dx}=\frac1c\cdot \sqrt{n(y)^2-c^2}$

干涉

杨氏双缝干涉

相干: $d\sin\theta = m\lambda,y=L\tan\theta \approx L\sin\theta=\frac{m\lambda L}{d}$

相消: $d\sin\theta = (m+\frac 12)\lambda,y=L\tan\theta \approx L\sin\theta=\frac{(m+\frac 12)\lambda L}{d}$

半波损

光疏到光密有半波损

$n_1<n_2$

半波损说明相位落后 $\frac{\lambda}2$

相位领先 $\phi$ 说明要 $-\phi$

$\cos(kx+wt)\to \cos(kx+wt-\phi)$

等倾薄膜干涉

alt text

$2nh\cos i=m\lambda, maxima$

$2nh\cos i=(m+\frac12)\lambda, minima$

对于垂直入射:

只有前反射面有半波损: $2nd+\frac12\lambda = m\lambda$
前后反射面都有半波损: $2nd = m\lambda$

等厚薄膜干涉

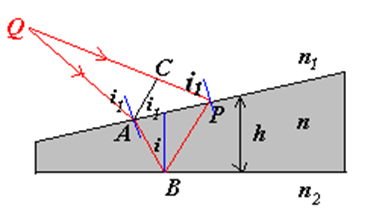
alt text

$2nh\cos i=m\lambda, maxima$

$2nh\cos i=(m+\frac12)\lambda, minima$

牛顿环

通过测量球面一部分的干涉纹来计算原本球的半径

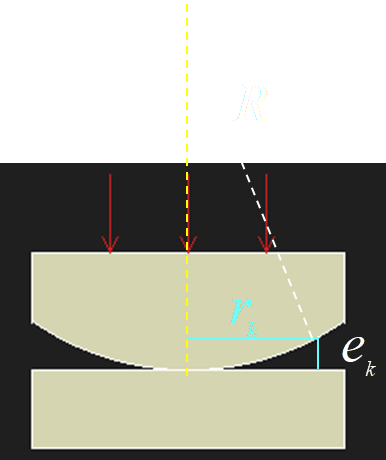
alt text

$\Delta L = 2h+\frac\lambda 2=\left\{\begin{array}{l}m\lambda & maxima\\\\ (2m+1)\frac{\lambda}{2} & minima\end{array}\right.$

注意由于是球面下的空气产生光程差，所以下反射面有半波损

$h=e_k=R-\sqrt{R^2-r_k^2}$

Michelson's Interferometer

$\Delta L=2d=m\lambda$

以太

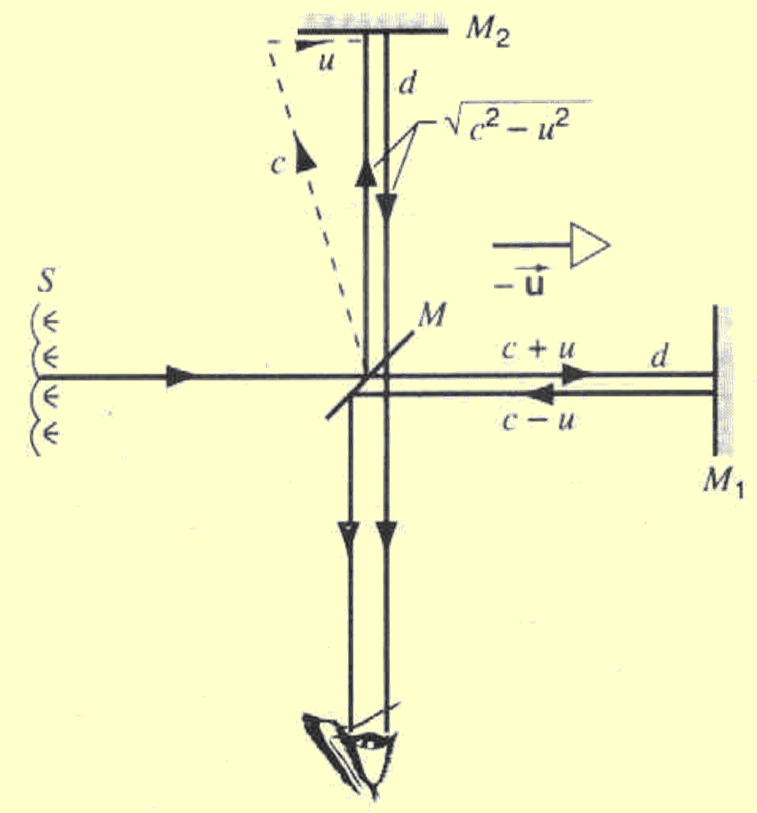
alt text

如果改变装置运动的方向, 理论上来说, 两个光线的光程差会因为以太运动方向不同而改变, 因此干涉条纹变化

但实验结果是, 无论怎么转, 干涉条纹不变

所以 以太不应该存在.

解决了物理学两朵乌云的第一朵

衍射

惠更斯原理

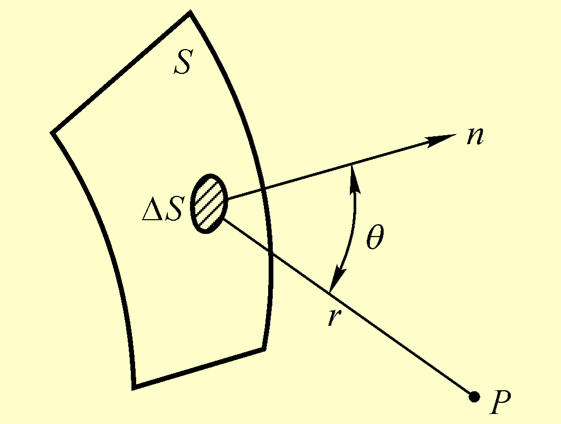
alt text

\[dE_p=C\frac{dS}{r} K(\theta)\cos(\frac{2\pi}{\lambda}r-\omega t+\phi_0)\]

波前的每一点可看作是新的波源

当光波遇到障碍物或狭缝时, 障碍物的边缘会成为新的波源, 从而使光波在原本的直线传播方向外传播 $\to$ 衍射

单缝

$n$ 条光线聚焦在一点

对应的相位差为 $\displaystyle \alpha = \frac n2 \Delta\phi$

且 $\displaystyle \Delta\phi = \frac{2\pi}{\lambda} \Delta x\sin \theta=\frac{2\pi}{\lambda} \frac{a}{n}\sin \theta$

所以 $\displaystyle \alpha = \frac{\pi a \sin \theta}{\lambda}$

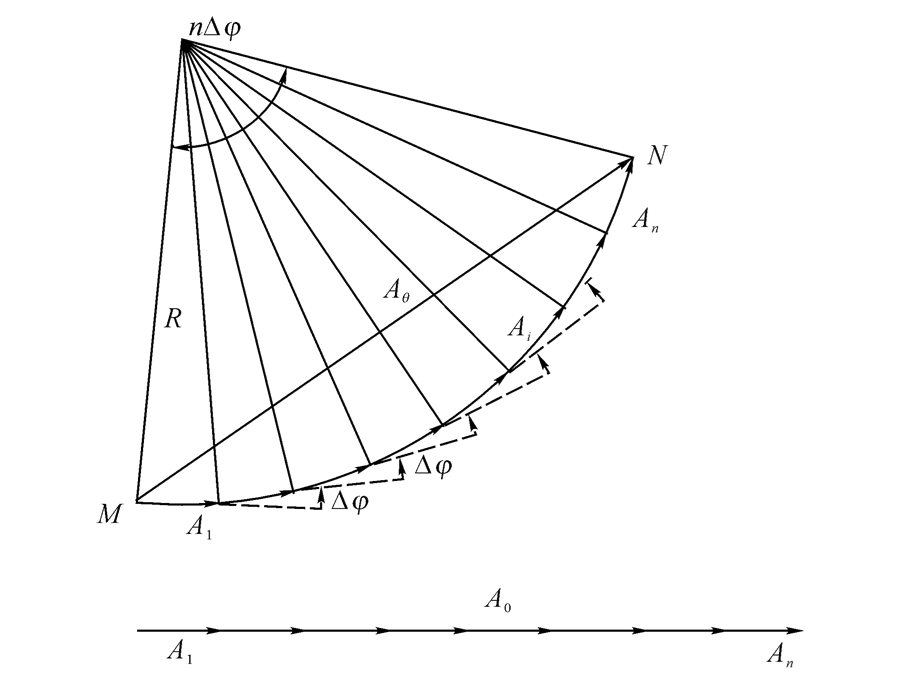
alt text

光强是电场平方: $\displaystyle I_\theta = E_\theta^2$

圆弧长对应最大的电场 (因为没有向量抵消)，弦长等于当前 $\theta$ 对应的电场

$E_m=\overgroup{MN}$

$\displaystyle E_\theta=\overline{MN}=E_m\frac{\sin\alpha}{\alpha}$

当 $\theta=0$, $E_\theta$ 能取到最大, $E_\theta = E_m$

$\displaystyle I_\theta=I_m(\frac{\sin\alpha}{\alpha})^2$

极大

中间零级最大是主极大

$a\sin\theta=m\lambda,minima$

$a\sin\theta\approx(m+\frac 12)\lambda,maxima$

用 $\frac{d}{d\alpha}(\frac{\sin\alpha}{\alpha})=0,\alpha=\tan\alpha$

$\alpha=\pm1.43\pi,\pm2.46\pi,\pm3.47\pi,\cdots$

可以看到越来越接近 $m+\frac 12$

$m=\frac{\alpha}{\pi}-\frac12=0.5,0.93,1.96,\cdots$

可以看到越来越接近整数 $1,2,\cdots$

半角宽度

$a\sin\theta = \lambda,\Delta\theta\approx\sin\theta=\frac{\lambda}{a}$

$\Delta y_m=f\cdot \Delta \theta = f\cdot \frac{\lambda}{a}$

圆孔

一级最小: $\sin \theta = 1.22\frac{\lambda}{D}$

瑞利判据

分辨临界, 当最小与最大重合

$\theta_R= \theta_{min}=1.22\frac{\lambda}{D}$

分辨本领: $R=\frac{1}{\theta_R}$

双缝

$n$ 条缝

缝与缝之间间距 $d$

$\displaystyle \delta = \frac{2\pi}{\lambda}d\sin\theta=2\beta$

$\displaystyle \beta = \frac{\pi d\sin\theta}{\lambda}$

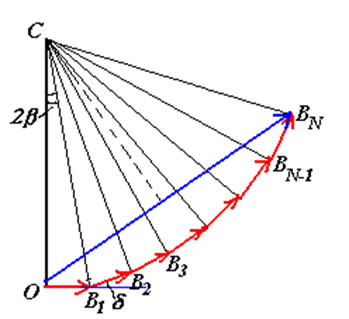
alt text

$\displaystyle E_\theta = \overline{OB_N}=2\overline{OC}\sin{N\beta}=2\frac{E_1}{2\sin\beta}\sin{N\beta}=E_1\frac{\sin N\beta}{\sin\beta}$

$\displaystyle E_1=E_m\frac{\sin\alpha}\alpha$

$\displaystyle \therefore I_\theta = I_m(\frac{\sin\alpha}{\alpha})^2(\frac{\sin N\beta}{\sin\beta})^2$

当 $N=2$ 时, $\displaystyle (\frac{\sin N\beta}{\sin\beta})^2=(2\cos\beta)^2$

$\beta$ 是干涉项, $\alpha$ 是衍射项

主极大

$\beta=m\pi,d\sin\theta=m\lambda$

两个主极大间有 $N-1$ 个次极小, $N-2$ 个次极大

主极大半角宽度 $\displaystyle\Delta\theta=\frac{\lambda}{Nd\cos\theta}\approx \frac{\lambda}{Nd}$

且由于 $\frac{\sin\alpha}{\alpha}$, 每 $d/a=n$ 个主极大都会出现一个主极大缺失

对于 $d=3a,N=4$:

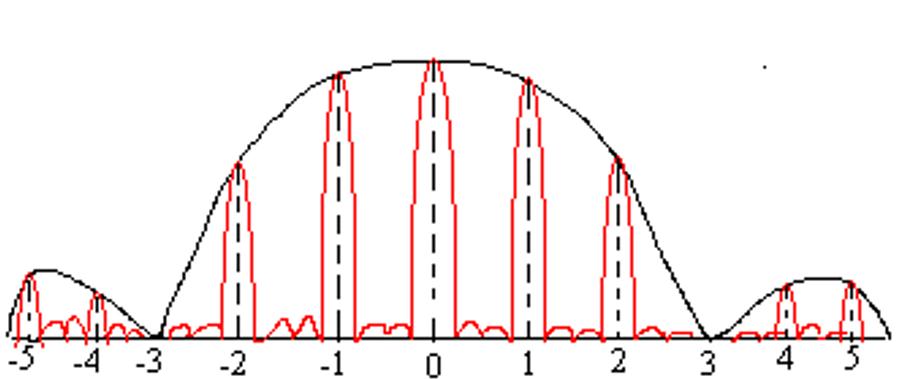
alt text

每两个缺失之间包含 $2n-1$ 个主极大,成为 diffraction envelope

色散本领

由 $d\sin\theta=m\lambda$

$d\cos\theta\Delta\theta=m\Delta\lambda$

$\displaystyle D=\frac{\Delta \theta}{\Delta \lambda}=\frac{m}{d\cos\theta}$

表示单位波长差可以分开的两个极大的角度差

分辨本领

$\displaystyle \Delta \theta_w=\frac{\lambda}{Nd\cos\theta}$

$\displaystyle \Delta \lambda = \frac{\Delta \theta_w}{D_\theta}=\frac{d\cos\theta}{m}\cdot \frac{\lambda}{Nd\cos\theta}=\frac{\lambda}{Nm}$

分辨本领 $\displaystyle R=\frac{\lambda}{\Delta \lambda}=Nm$

与 $d$ 无关, 只与 $N,m$ 有关

代入半角宽度是因为这是最大的宽度, 所以是最严苛的条件

$\Delta \lambda$ 表示两束光的波长差

$\lambda$ 表示波长短的光波长

光栅

Bragg's law

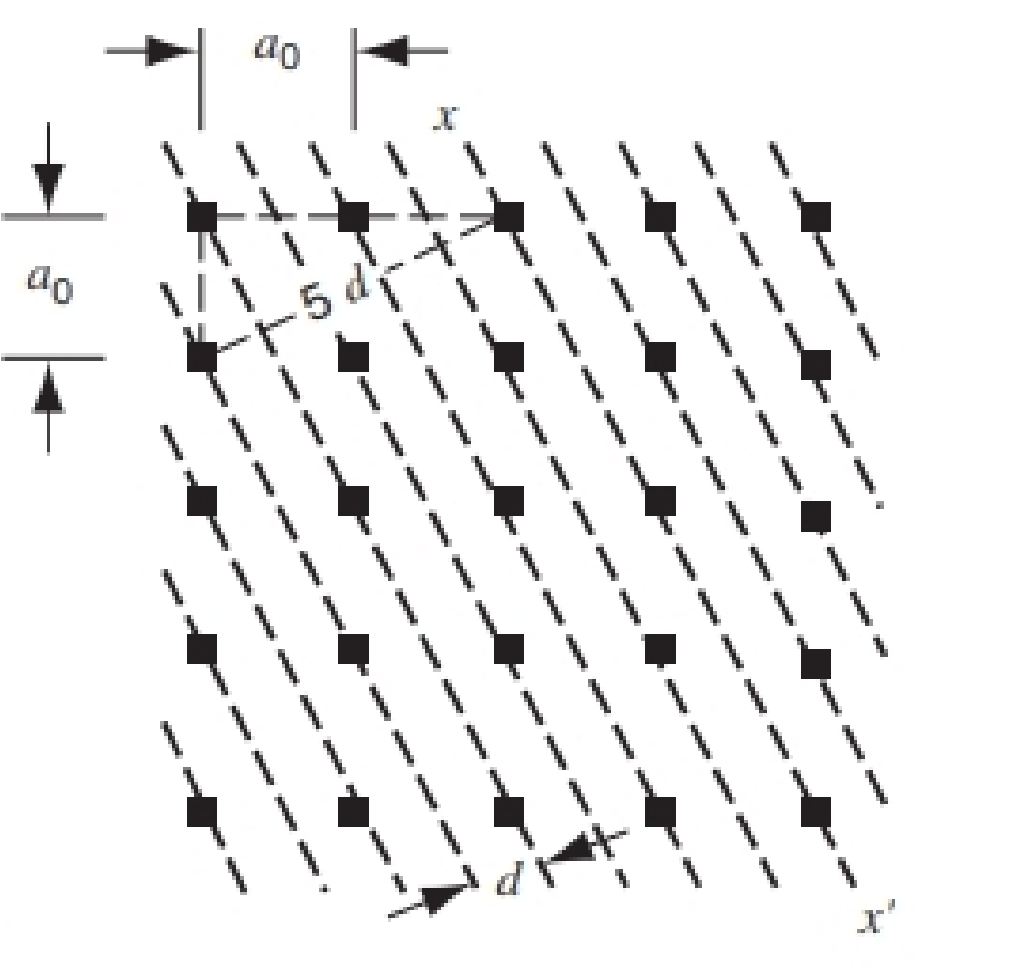
晶体中 $2d_0\sin\theta = m\lambda$

$d_0$ 是分子间距

在晶格中, 晶面间距 (interplanar spacing) 为 $d=\frac{d_0}{\sqrt{h^2+k^2}}$

$h,k$ 互质

例如 $h=2,k=1$:

alt text

偏振

偏振方向 = 电场方向

Law of Malus

自然光通过偏振片后光强变为 $1/2$

$\displaystyle dI=I\cos^2\theta\frac{d\theta}{2\pi}$

除以 $2\pi$ 表示某一方向的光强期望

所以对于 $\cos^2\theta$ 从 $[0,2\pi]$ 积分, 得到 $\pi$, 所以 $I'=I\pi\cdot\frac{1}{2\pi}=\frac{I}2$

Brewster's angle

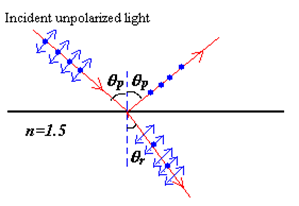
alt text

$\tan\theta = \frac{n_2}{n_1}$

双折射

$O, E$ 光

$O$ 光: 光的电场方向与光线与光轴构成的平面垂直

$E$ 光: 光的电场方向与光线与光轴构成的平面平行

波片

$E$ 光比 $O$ 光领先 $1/4, 1/2$ 个周期

领先 $1/4\lambda, 1/2\lambda$

光程差: $\Delta L = (n_e-n_o)d$

相位差: $\Delta \phi = \frac{2\pi}{\lambda}(n_e-n_o)d$

例如, 线偏振光:

$E_x=E_0\sin(kz-\omega t)$

$E_y=E_0\sin(kz-\omega t)$

经过 $1/4\lambda$ 波片:

假设光轴是 $x$ 轴

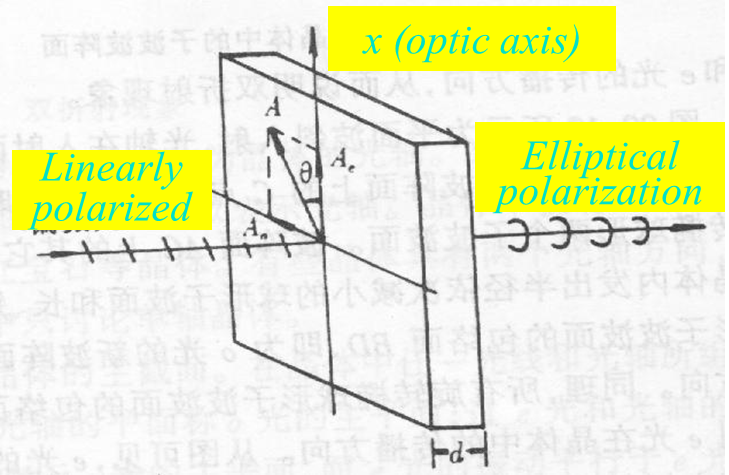
alt text

与光轴, 传播方向所成平面垂直的 $y$ 方向为寻常光

$A_o$ 相位不变, 即相位 $\alpha_{slow}\to \alpha_{slow}$

$A_e$ 快了 $1/4$ 周期, 即相位右移, $\alpha_{fast}\to\alpha_{fast}-\frac{\pi}{2}$

所以

$E_x=E_0\sin(kz-\omega t)$

$E_y'=E_0\sin(kz-\omega t-\frac{\pi}{2})$

变成圆偏振光

区分圆偏振与自然光

圆偏振与自然光通过偏振片, 转动偏振片, 光强都不变

但如果前面加一个 $1/4\lambda$ 波片, 圆偏振光通过后变成线偏振光, 再通过偏振片有消光

而自然光通过波片是许多圆偏振光叠加, 再通过偏振片强度不变

区分所有种类的偏振光

单独使用偏振片

旋转偏振片
圆偏振光/自然光: 光强不变
线偏振光: 变, 有消光
椭圆偏振光/部分偏振光: 变, 无消光
使用 $1/4\lambda$ 波片 + 偏振片

旋转偏振片

自然光 $\to$ 自然光 $\to$ 线偏振光: 光强不变
圆偏振光 $\to$ 线偏振光 $\to$ 线偏振光: 变, 有消光

部分偏振光 $\to$ 部分偏振光 $\to$ 线偏振光: 变, 无消光
椭圆偏振光 $\to$ 线偏振光 $\to$ 线偏振光: 变, 有消光

散射

原理: 光通过分子, 使价电子振动, 再发出光, 产生散射光

散射光是偏振光

光的本质

光电效应

$h\nu=\frac12 mv^2+\phi=eV_0+\phi$

$\phi$ 是逸出功 (work function)

极限频率: $h\nu_0=\phi$

截止电压与频率关系: $V_0=\frac{h}{e}\nu-\frac{\phi}{e}$

黑体辐射

物理学的第二朵乌云

普朗克辐射定律

$\displaystyle R(\lambda,T)=\frac{2\pi hc^2}{\lambda^5}\frac{1}{e^{\frac{h\nu}{kT}}-1}=\frac{2\pi hc^2}{\lambda^5}\frac{1}{e^{\frac{hc}{\lambda kT}}-1}$

Wien's Law

当强度达到最大的波长满足: $T\lambda_m=b$

同时满足 $\frac{h\nu}{kT}=2.82$

量子力学

$\Psi$ 函数

求函数 $U(x)$ 的平均值:

$\displaystyle \int_{-\infty}^{\infty}\Psi U(x)\Psi^*dx=\overline{U}(x)=\langle \Psi \vert U(x)\vert \Psi \rangle$

Schrödinger equation

构造

1. 两种算符

能量算符 $i \hbar \frac{\partial}{\partial t}$

动量算符 $-i \hbar \frac{\partial}{\partial x}=-i \hbar \nabla$

2. 平面波方程

$E(r,t)=E_0e^{i(kr-\omega t)}$

3. `de Broglie` 关系

$E=\hbar \omega, p=\hbar k$

4. 开始构造

将 de Broglie 关系式带入平面波方程得出一般自由粒子波方程

$\Psi (r,t)=Ae^{\frac i \hbar(pr-E t)}$

又有 $\int_{\infty}|\Psi(r,t)|^2dr=1$ 归一化，得到系数$A=(2\pi \hbar)^{-3/2}$

之后，将两种算符作用于波方程：

$i \hbar \frac{\partial}{\partial t}\Psi = E\Psi$

$-i \hbar \nabla \Psi = p \Psi$

动量算符作用两次：

$- \hbar^2 \nabla^2 \Psi = p^2 \Psi$

同除以 $2m$ 得到：

$- \frac{\hbar^2}{2m}\nabla^2 \Psi = \frac{p^2}{2m} \Psi$

由于能量等于动能加势能：

$E=\frac{p^2}{2m}+V(r,t)$

所以 $i \hbar \frac{\partial}{\partial t}\Psi(r,t)=(- \frac{\hbar^2}{2m} \nabla^2+V(r,t))\Psi(r,t)$

令 Hamilton 算符为 $\hat H=- \frac{\hbar^2}{2m} \nabla^2+V(r,t)$

则 $i \hbar \frac{\partial}{\partial t}\Psi(r,t)=\hat H\Psi(r,t)$ 为薛定谔方程

注：$|\Psi(r,t)|^2$ 表示粒子在某位置某时间出现的概率

进一步, 将 $\Psi(r, t)$ 展开为 $\Psi(r)e^{-i\omega t}$

$i \hbar \frac{\partial}{\partial t}\Psi(r,t)=(- \frac{\hbar^2}{2m} \nabla^2+V(r,t))\Psi(r,t)\to i \hbar (-i\omega) \Psi(r)e^{-i\omega t}=(- \frac{\hbar^2}{2m} \nabla^2+V(r,t))\Psi(r)e^{-i\omega t}$

$\hbar\omega \Psi(r)=(- \frac{\hbar^2}{2m} \nabla^2+V(r,t))\Psi(r)$

并且 $V(r,t)=V(r)$

所以 $E \Psi(r)=(- \frac{\hbar^2}{2m} \nabla^2+V(r))\Psi(r)$ 为定态薛定谔方程

~~图源：Minghu Fang PPT~~

环路与面公式

定义

散度

旋度

静电场

Stokes 公式

电场环路定律

通过 Stokes 公式, 电场环路定律推出微分形式

Gauss 公式

Gauss 电场定理

通过 Gauss 公式, Gauss 电场定理推出 Gauss 电场定律微分形式

恒磁场

Ampere 磁场环路定律

Gauss 磁场定理

同样用两个数学公式推导出微分形式

电偶极矩/磁偶极矩

电偶极矩

磁偶极矩

电位移矢量 (电感应强度) 高斯定理

磁场强度高斯定理

介电常数

\(\kappa_e\geq 1\)

介质中的电场

电流密度

能量密度

能量

弹性势能

动能

电容能量

电感能量

电场能量

磁场能量

球坐标下的算子

梯度

散度

旋度

柱坐标下的算子

梯度

散度

拉梅系数

电学物理量与电荷，距离关系

有关符号

电场强度 \(E\)

点电荷

长直导线

圆环

圆盘

无限大极板

电偶极矩

电势能 \(U\)

球壳

一般求法

两两配对

电势 \(V\)

圆环

圆盘

电容 \(C\)

球壳

空球壳

一般化

平行板

圆柱体

磁感应强度 \(B\)

电流元

长直导线

圆环

螺线管

螺绕环

无限板

磁偶极矩

电感 \(L\), 互感 \(M\)

无限长螺线管

长方形螺绕环

同轴电缆

电感与互感

\(RC\) 电路

\(RL\) 电路

通电

放电

\(LC\) 电路

`Euler-Lagrange` 方程

3. `de Broglie` 关系