submodular

AKonjac_

2025-07-28 (Updated: 2025-10-25)

submodular function

definition

submodular

对于和元素 , 有

也即函数的离散导数单调不增

另一种定义为:

对于任意集合有

对于第一种定义, 即转换为第二种定义

supermodular

与 submodular 符号反过来

modular

Lovász extension

将次模函数转换成连续凸函数 :

看着很乱, 给个例子

$例$

对于一个次模函数 , 定义域为 :

$，$

可以用图左边表示

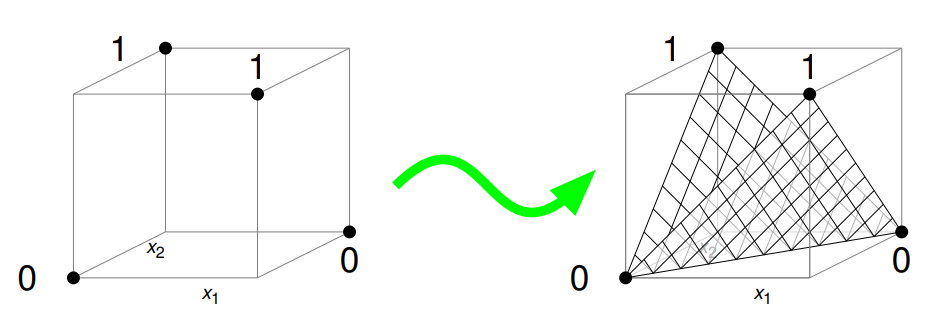
alt text

读者可以验证次模性

并且通过 Lovász extension 转换成 , 对应图右边

解释一下这个图

对于的情况, 就是下面这条线

因为集合只可能是 , 所以这条线上

对于不在线上的点, 例如图中

那么对于均匀分布的 ,

所以期望是

由图可以看出凸性, 也可以证明凸性

事实上 , 是凸函数

concavity or convexity

细心的读者可能发现了, 次模的定义看起来更像凹函数, 但上面的是凸函数, 可以求最小值, 并且可以转换成的最小值

并且你可能也发现, 次模函数不仅仅能转成凸函数, 上面的例子翻上去就是凹函数:

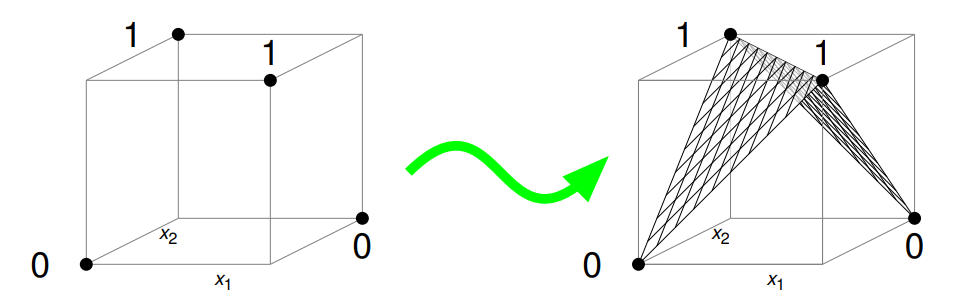
alt text

所以不同角度来看, 次模函数分别有着凸的方面与凹的方面, 其中凸性很重要

事实上对于凹性, 最大化的问题往往难以求解, 如 Max Cut 的目标函数是次模函数是 NP-Hard

greedy algorithm (discrete)

对于求解单调的次模函数最大值, 有贪心算法:

当前集合为空, 第一次迭代选择收益最大的节点并加入集合, 即

其中有限制

有近似比

$证明$

假设最优的集合为

由于单调性, 我们不妨假设最优的集合刚好有个元素

那么由单调性, 如果我们将中的元素依次加入当前集合 :

这一步由于次模函数的性质

这一步由于第步加入的是受益最大的点, 任何的收益都小于等于这个值

这一步因为

所以记

有

所以

取则有的近似比

也可参考这篇文章

multilinear relaxation

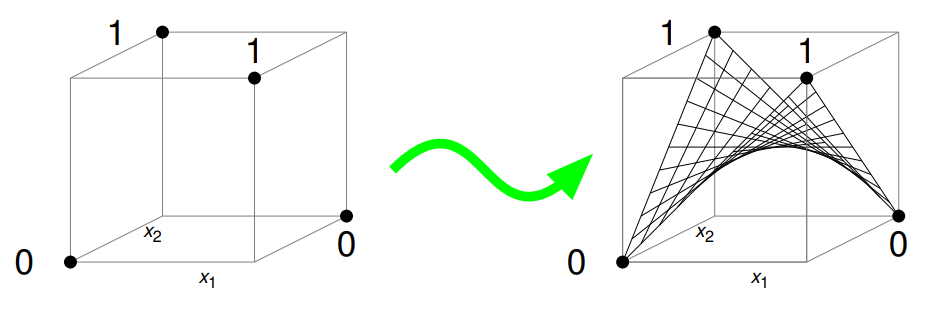
alt text

greedy algorithm continuous

matroid

kruskal

最小生成树

Kuhn-Munkres

匈牙利算法

k-submodular

definition

给一个有限非空集合 , 以及正整数

函数定义在个不相交的的子集上

即

即每个的元素要么属于集合 , 要么谁也不属于

将表示为向量

如果 , 说明属于

(可以表示成 )

对于 , 我们说如果

对于 , 我们说他是 k-submodular 的, 如果

其中

说他是 monotone 的, 如果

参考: