Shortest Processing Time

(Updated: )

local search 是 2 近似

将任务任意放进机器中, 如果最晚完成的任务的起始时间可以提前, 即某个机器在这个任务开始前已经空闲, 就将这个任务挪到空闲机器中

这是一个 local search

并且每个任务最多挪动一次, 即 local search 可停止

不严格证明近似比了, 给个例子: 构造一个 个 , 个 的例子

其中

那么如果有 个机器, 那么最优解是

而 local search 可能得到 个机器各放一个 , 一个机器放了所有的 个 , 最后一个机器放了 个

那么这个解为

所以近似比是

可以任意小

LSA (List Scheduling Algorithm) 是 2 近似

LSA 是贪心算法, 将任务任意排序, 然后按照机器空闲时间最早的顺序放入任务

那么这个贪心得到的解就是 local search 停止时的情况

所以他也是 近似的

LPT (Load Processing Time) 是 4/3 近似

就是将 LSA 的任务从大到小排序, 之后再按机器空闲时间最早的顺序放入任务

这个算法是 近似的

具体地, 我们要证明如下定理:

定理 有 个任务, 台机器. 如果 LPT 算法给出的处理时间为 , 最优解为 , 那么

并且这个界是紧的

证明

反证

所有任务从大到小依次为

假设

如果我们在处理到 时达到最大值 , 那么考虑集合 , 这个集合使用同样算法得出的解也是

同时由于任务变少, 最优解不会比之前差, 即

那么由 式

所以 是一个比 更小的输入

所以我们不妨找一个最小的输入, 即 的输入, 现在把它记为

于是我们有不等式:

这是因为最优解不会比所有任务平均执行时间短

并且如果记 为 开始执行的时间, 那么 , 以及

即在 开始前, 所有机器都是忙的

所以有

由 式,

这说明在 的假设下, 任何机器不能处理超过 个任务

接下来定义两种 local search 的调整策略 和

  • : 操作后 不增

    1. 当

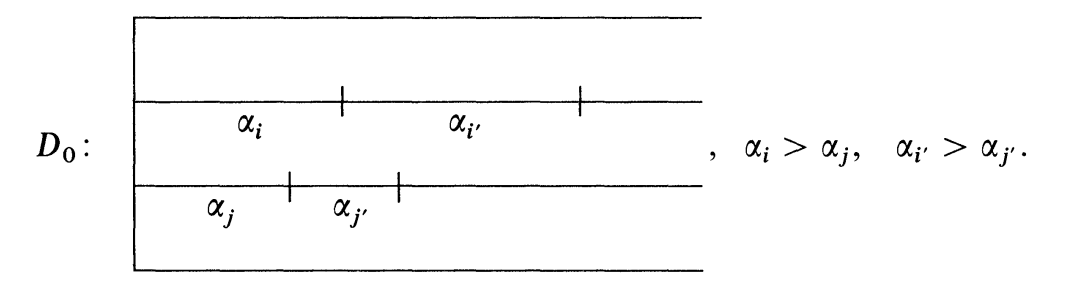
      alt text

      此时调换 , 那么解不会变差

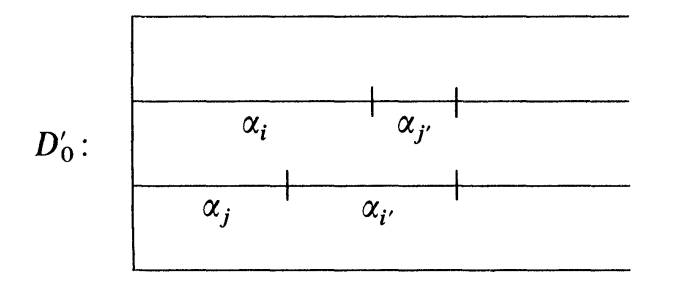
      alt text

    2. 当 被放在了处理时间更长的机器

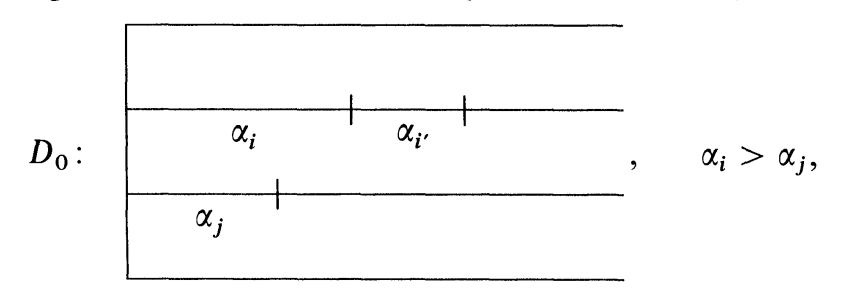
      alt text

      此时将 放入更早完成的机器, 解不会变差

  • : 操作后 不变

    只有交换同一列的两个任务

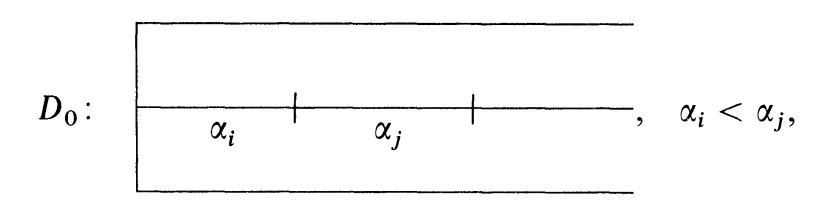
    alt text

    才保证了 不变

此时假设第 台机器的完成时间是 , 定义势能函数

那么 会使 , 会使

所以这个 local search 可以结束在某个状态 , 因为 会减少 , 所以只能操作有限次, 而两次 之间的 亦是有限的

并且这个 是最优解 的一种布局, 因为这种 local search 的操作可以覆盖机器处理不超过 任务的 SPT 问题的所有可能布局, 即它已经不是 local search, 而是 global search 了

这种情况得到的解是最优的

所以 满足:

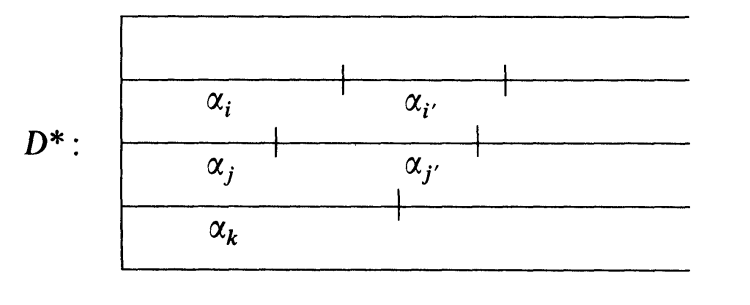
alt text

并且可以写成 :

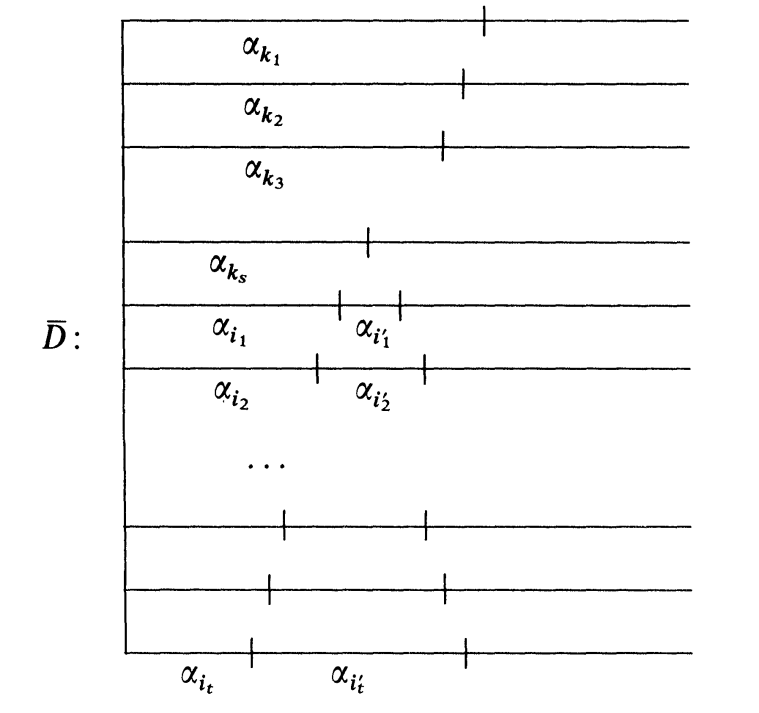
alt text

由 , 这些项满足

可以看出这个解的形式与 LPT 得出的解的形式一模一样

唯一可能的区别在于, 如果存在某个 , 即

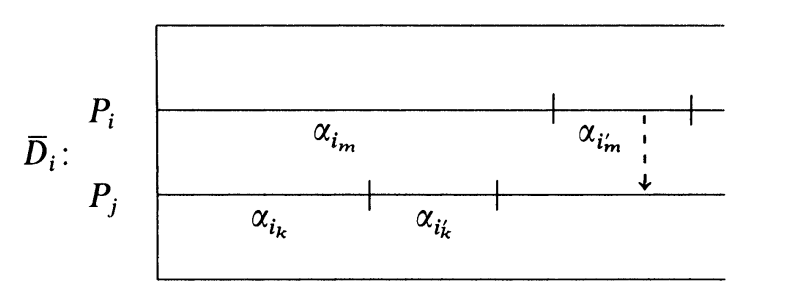
alt text

那么可以将 挪到 机器中, 但这与 的假设矛盾, 因为这样就有某个机器处理了 个任务

所以我们之前得到了 与 LPT 算法得到的 是等价的, 那么

但是这与 式的假设矛盾

所以反证得到 成立

为了说明这个界是紧的, 给出一个例子:

即

那么

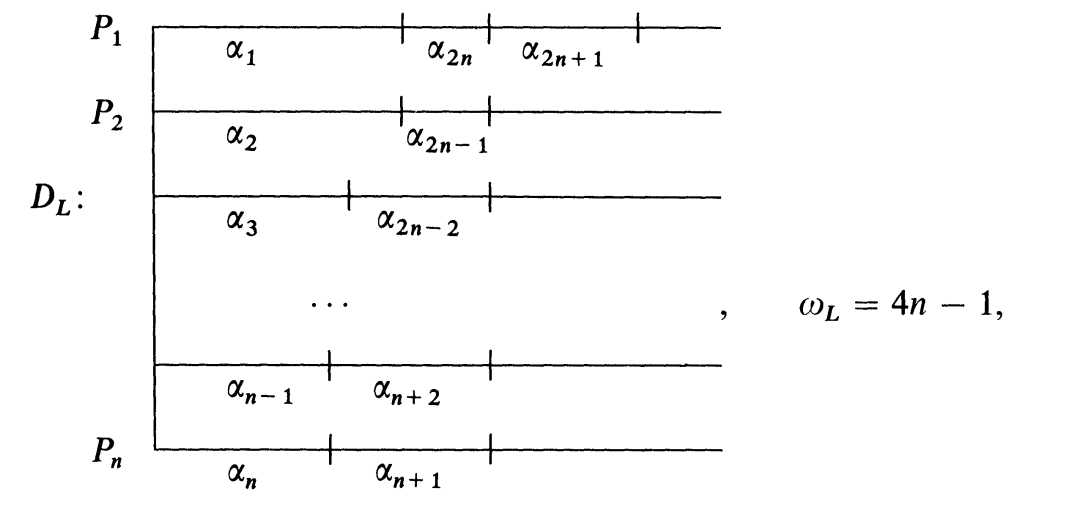
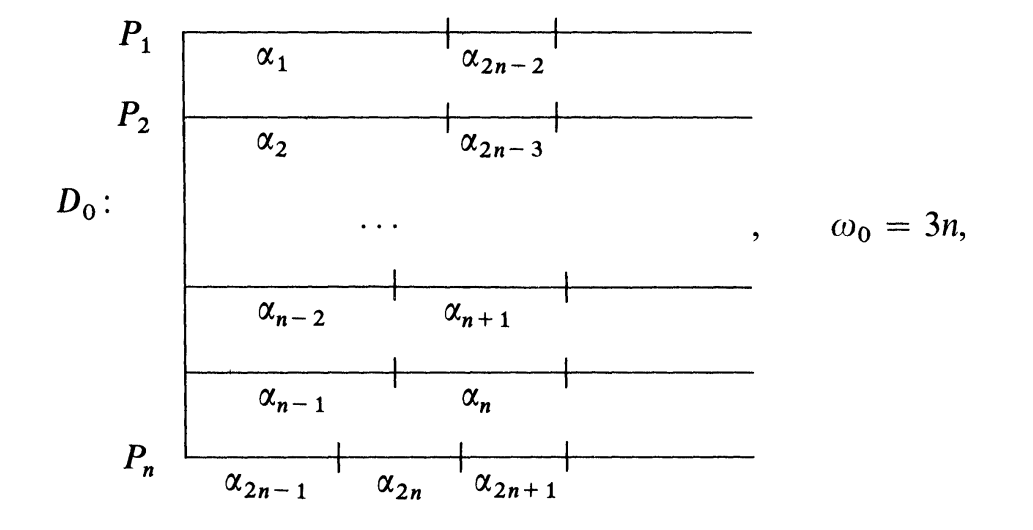
alt text

alt text

即

  • 对于上述证明中使用策略 的 local search 方法, 如果用在一般的 SPT 问题中 (即机器可以处理超过 任务), 他是多项式时间的最优算法吗?

    : 最优应该可以保证, 因为这种 search 在一般的 问题中也可以遍历每一种布局

    但是多项式时间好像不行, 的第一种情况不像是多项式的

更一般的算法

我们可以按照之前的算法排序, 将前 大的任务按顺序分配给最早空闲的机器, 然后将后 个任务按任意顺序分配给最早空闲的机器

定理

证明这个算法得到的解 满足:

并且在 时是最优的界 (紧的)

证明

令

那么对于最后的解 , 它最多是由 与之前的任务组成, 这一列之前的任务自身或加上某个 后刚好等于 , 所以他不应该在 之前空闲

即所有的任务时间加和要大于所有机器取这个下界 , 加上某一列加上了 后达到

并且

所以

由于一共至少有 个任务时长大于 , 所以鸽巢原理一定有某个机器处理了 个这种长任务

所以

所以

即定理中的不等式成立

对于在 时是紧的界, 可以给出一个例子:

假设算法选出的分配顺序是

所以算法得到的解为 ,最优解是

所以

由这个定理, 可以得出前一个定理的结论: 对于全排序的情况, 得出的解 好于排序前 个任务的解 , 所以

以及不排序的近似比:

参考:

  1. BOUNDS ON MULTIPROCESSING TIMING ANOMALIES