21 NPC problems

(Updated: )

langauge

包含所有 串的集合为

叫做 language

任何一个判定问题对应着一个

对于 , 表示字符串的长度

deterministic algorithm

一个确定性算法 包含:

  1. 可数集 (定义域)
  2. 可数集 (值域)
  3. 有限的字母表 ,
  4. 编码函数
  5. 转移方程

computation

的一个计算是对应输入 的唯一序列 , 使得 , 如果序列有限并且停在 , 那么

中间的这些 称为 instantaneous description

长度 称为 的运行时间

运行在多项式时间内, 如果

算法 计算的是函数

recognition algorithm

  1. 如果 , 那么 称为识别算法

    如果 则 称为字符串识别算法

    可被 识别的 language 为

  2. 如果 那么 被称为字符串映射算法

是一类可以多项式时间被确定性图灵机识别的 language, 即 的子集

是一类字符串映射函数, 满足

reducible

是 language

我们说 , 如果

Lemma 1: 如果 且 , 那么

因为存在一个多项式时间算法, 先计算 , 再在多项式时间识别是否 , 以此识别是否

  • 注意: 归约强调的是问题的类别 (计算复杂度); 对于问题的解, 一般要求存在性一一对应 (即 一一对应)

可数集上的

  1. 给出一对一编码 , 我们说 可以多项式时间被识别, 如果

  2. 并且, 给出 和 以及编码 和 , 那么 当且仅当

nondeterministic algorithm

一个非确定性算法 包含:

  1. 可数集 (定义域)
  2. 可数集 (值域)
  3. 有限的字母表 ,
  4. 编码函数
  5. 转移方程

注意 是一个映射的集合, 而不再是单个映射

对于 , 集合 元素不多于 个

computation

的一个计算是对应输入 的序列 , 使得 , 如果序列有限并且停在 , 那么

出现在某个计算中的 称为 instantaneous description

recognition algorithm

一个非确定性识别算法 包含:

  1. 可数集 (定义域)
  2. 有限的字母表 ,
  3. 编码函数
  4. 转移方程

的一个计算是对应输入 的序列 , 使得 , 如果序列有限并且停在 , 那么

结束在 的计算为被接受的计算

我们说输入 被接受, 如果 存在一个被接受的计算

如果 则 称为非确定字符串识别算法

并且 运行在多项式时间内, 如果当 接受 时, 存在一个接受的计算, 长度满足 , 即

表示 的可多项式时间识别的一类子集

令 , 构造

称 为从 中由多项式界存在量词 (p-bounded existential quantification) 导出的 language

就是说 是从 挑选出的 中的 组成的集合, 并且 是关于 的多项式

则 为从 的元素中由多项式界存在量词 (p-bounded existential quantification) 导出的 language 类

即

此为 定义

Theorem 1: 当且仅当 被多项式时间运行的非确定图灵机接受

非确定图灵机指, 当遇到了两个决策时, 可以将自身复制一份, 走向两个不同的分支 (重复分裂会导致指数级的复制体); 当任何一个决策路径指向 时即可判定 accepted

证明

如果 , 那么可以构造一个非确定图灵机, 来猜测 的每一位, 长度 , 再判断是否 , 这样的机器可以在多项式时间接受

如果 可被多项式时间运行的非确定图灵机 接受

假设对于一个 instantaneous description , 最多有两个后继的

那么这样的 的决策序列对应着 字符串 , 且

那么可以构造一个确定性图灵机 , 定义域是 , 对于输入 模拟 对应的决策

这样的图灵机可以在多项式时间内运行, 从而 可以通过 模拟所有被 接受的字符串 得到, 并且 的运行时间是多项式内的

所以 是由多项式界存在量词导出, 即

SAT

一些定义

query machine

一个 Turing machine, 有一个 query tape, 和三个状态 query state, yes state, no state.

-computation

是一个 query machine, 是一组串, 那么 -computation 定义为:

初始 在 initial state, 输入为 ; 每次 进入 query state, tape 上有一个串 , 那么 下一个状态为 yes, 当且仅当 ; 状态为 no 当且仅当

-reducible

一组串 可以多项式归约到一组串 , 当且仅当存在 query machine 和多项式 , 使得对于机器 , 输入为 的 -computation 在 步内结束, 并且当且仅当 , 停机在 yes state

DNF

是串集合, 可以表示所有 DNF 永真式

代表着最多有 个 CNF 的 DNF

证明 SAT

Theorem 2: 证明如果一组串 可以被非确定图灵机用多项式时间接受, 那么 可以多项式归约到

证明定理 2 后立即得到任何 问题可以归约到 SAT, 因为如果 , 那么 可被非确定图灵机用多项式时间接受

证明

假设非确定 Turing machine 在多项式时间 内接受一组串

对于机器 的一个输入 , 构造一个 DNF , 那么 是永真式当且仅当 接受

由于 的构造关于 是多项式, 所以构造出这样的 即完成证明

我们可以假设 tape 上有从左到右从 到无穷编号的方块, 输入 长度为 , 包含 个方块

且 在 步后进入接受状态

假设字母表 , 状态集合为

定义几个表达式:

  1. 表示在第 步时, 第 个方块包含字母
  2. 表示在第 步时 状态为
  3. 表示在第 步时方块 被 扫描到 (输入)

那么给出

  1. 断言每一步 有且仅有一个方块被扫描到

    我们有

    其中

    意思就是至少有一个方块, 且任意两个方块最多有一个在同一时刻扫描到

  2. 对于

    断言在第 步, 第 个方块有且仅有一个字母

    “有且仅有一个” 使用与 相同的表示方式

    是所有 合取

  3. 断言每一步 机器有且只有一个状态

  4. 断言初始状态满足:

    其中 , 是空字母, 是初始状态

  5. , , 断言每一时刻 的值是及时更新的

    例如 断言在第 步状态为 , 扫描到了字符 , 那么第 步状态为 , 是满足 转移方程的 的后继

  6. 断言机器一定会结束在接受状态

至此完成 的构造, 并且 满足前文的性质

因此证毕

同时, 原文 一共定义了 个问题, 并且有如下推论:

corollary 1: 所有 个问题的定义对应的串集合都可以归约到

这是因为这 个问题都可以由非确定图灵机在多项式时间内接受

Complete

定义

是完备的, 如果

  2. SAT

可数集上的

是可数集, 是一对一编码 并且

那么 完备当且仅当 完备

Lemma 2: 给出可数集 ; 和 以及一对一编码 和 , 那么 , 如果存在一个函数 使得

  2. 存在一个函数 使得 , 当 有定义时

    即

21 个问题

定义

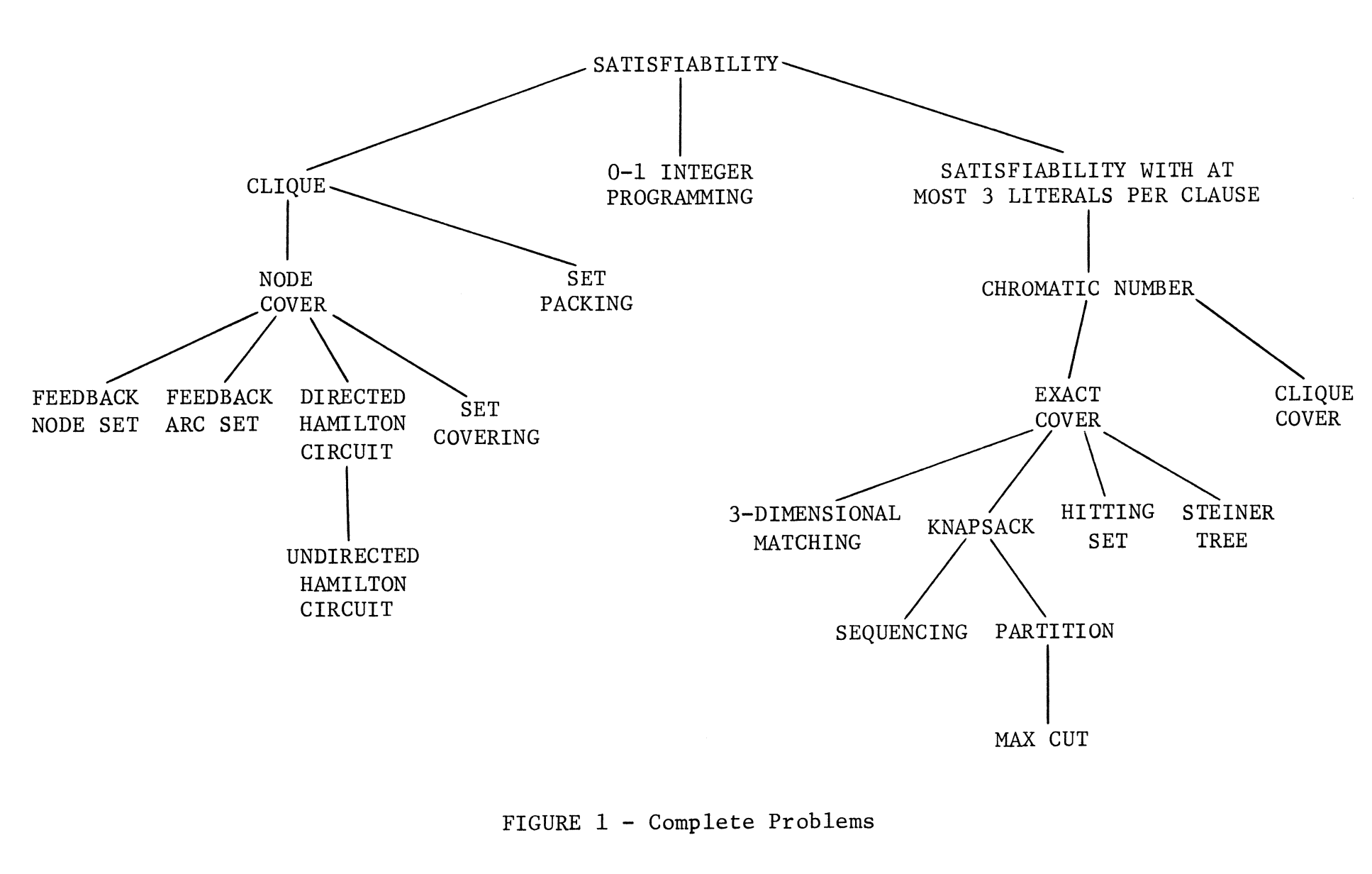
alt text

alt text

alt text

归约

alt text

  1. SAT 0-1 integer programming

    alt text

    例如对于一个子句 为 的条件是

    所以

    即

    所以如果存在 满足 , 说明 SAT 问题可满足, 因此 SAT 问题可归约到 0-1 IP

    • 注意: 上面 0-1 IP 问题的定义能否改成 ?

      (因为说到 “规划” 问题, 如线性规划, 一般都是不等式约束条件)

  1. SAT clique

    alt text

    每个子句建出 个点, 一共 个子句, 个点

    同时, 同一个子句之间的点没有连线, 互为补的两个字符对应的点也没有连线

    那么如果原图有 的团, 一定满足每个点恰好来自于一个子句, 并且两两不互补

    这样就可以调控各字符的取值, 使得 SAT 可满足

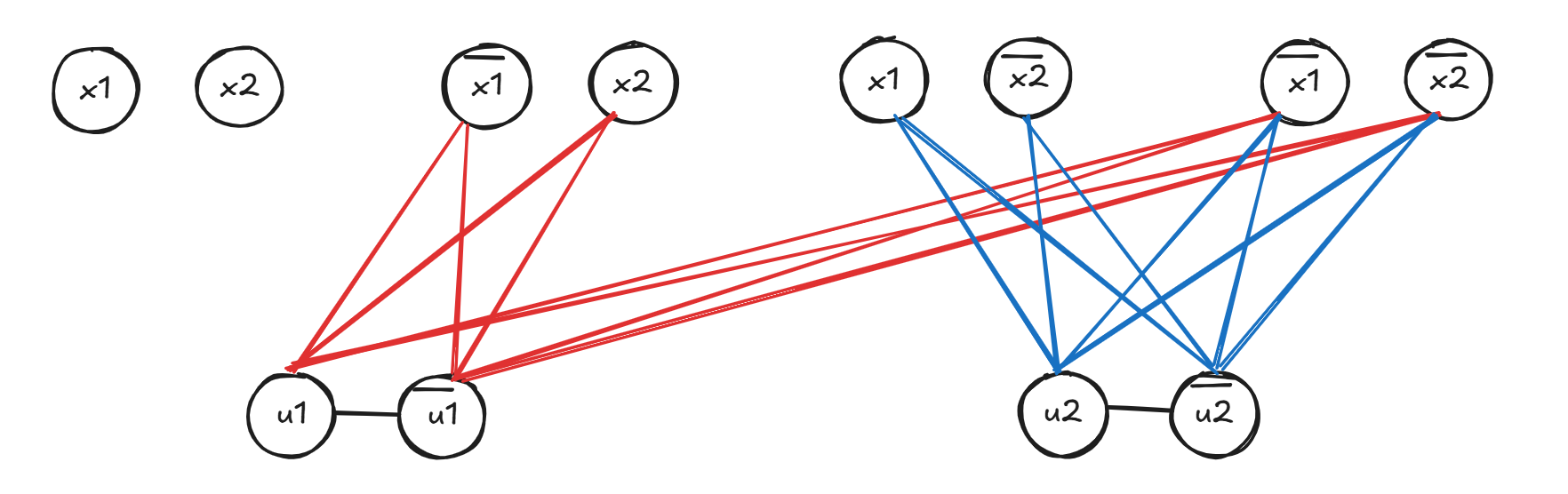
    一个例子:

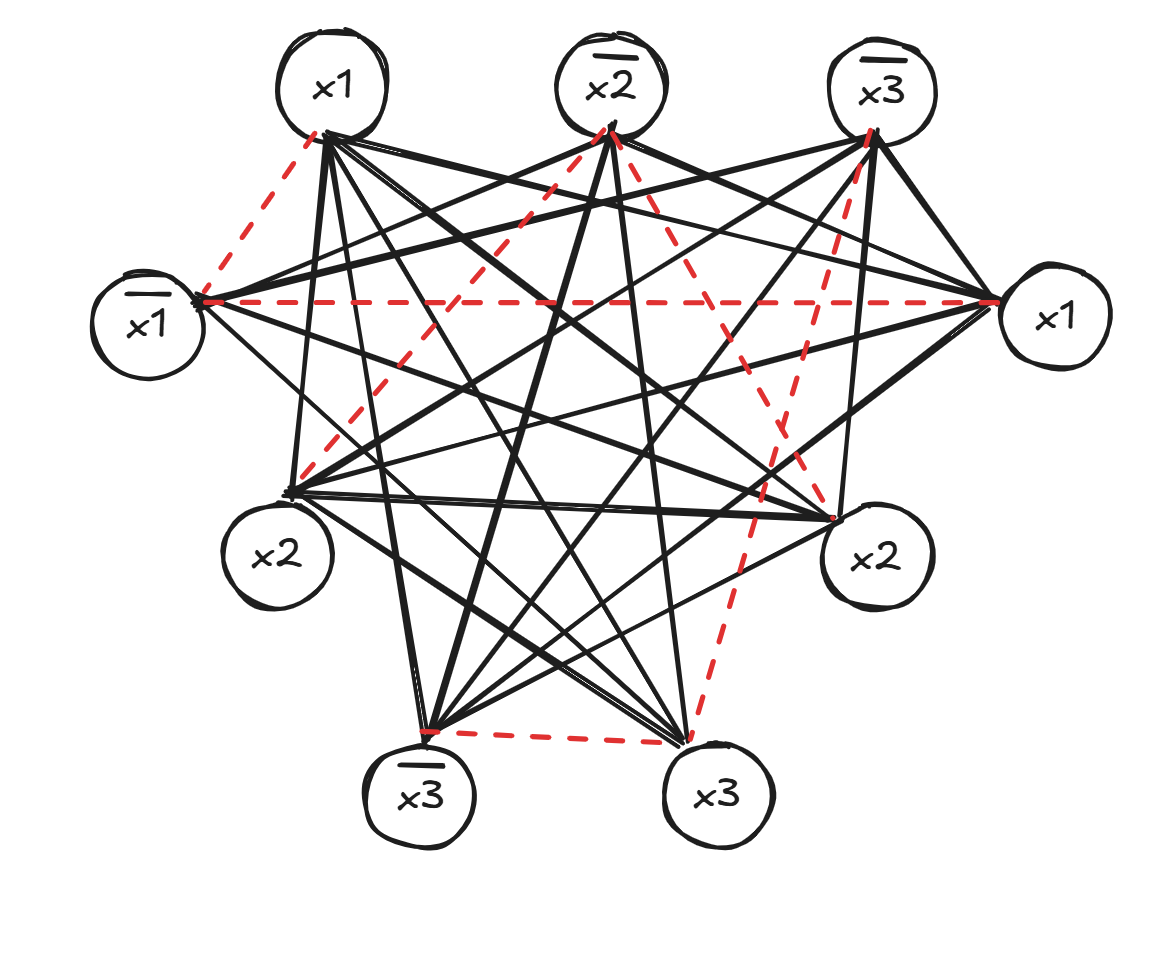
    alt text

    图中红色线是互补的两个点省去的线

    由于有 个子句, 所以只要有三角形, 就说明原图有 的团, 则 SAT 可满足

  2. clique set packing

    alt text

    建一个反图, 表示反图的邻接表

    那么如果反图中有 个互不相交的集合, 说明集合对应的点两两不相连, 那么在原图中这些点一定是两两相连, 所以这 个点构成一个团

  3. clique node cover

    alt text

    建一个反图, 反图中如果有一个 的顶点覆盖 , 那么反图的每条边都至少与一个 中的点相连, 则原图中的每一条边都不与 中的任何一点相连, 所以原图中的所有边一定都连接着 中的点

    并且一定是两两之间有边, 不然会存在一条反图中不与任何 中点相连的边

    所以 中的点构成一个团, 大小

  4. node cover set covering

    alt text

    把图中的邻接表 选出 个, 如果能够覆盖所有边, 说明这 个集合对应的点是原图的一个大小为 的顶点覆盖

  5. node cover feedback node set

    alt text

    直接把原图改成双向的有向图

    注意双向的有向边组成了两个点的环, 所以如果这些环都经过了某个 中的点, 说明在原图中所有边都被 中的点覆盖

  6. node cover feedback arc set

    alt text

    复制一份图, 同一个点两两连接, 并且对于原图中有的边, 从 号图向 号图连边

    那么在新图中选择相同编号的点之间的边, 就相当于在原图中选择了这个点, 所以就从选点归约到了选边

  7. node cover directed hamilton circuit

    alt text

    这个太妙了, 只能用个例子讲了

    如果 node cover 中 原图 为:

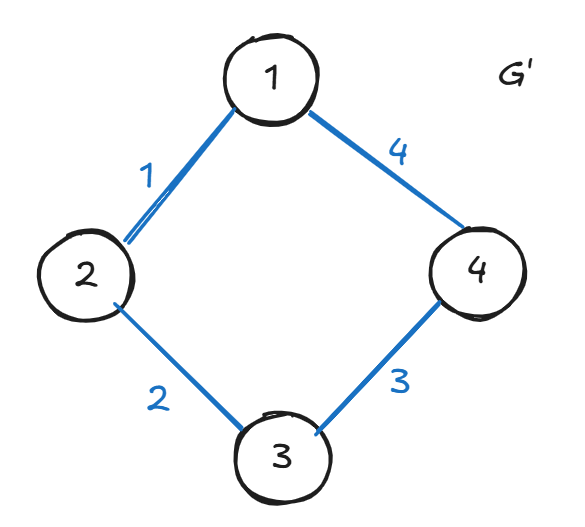
    alt text

    其中边集对应的编号是 , 即为 的整数集, 是 边的个数

    那么构造一个有向图:

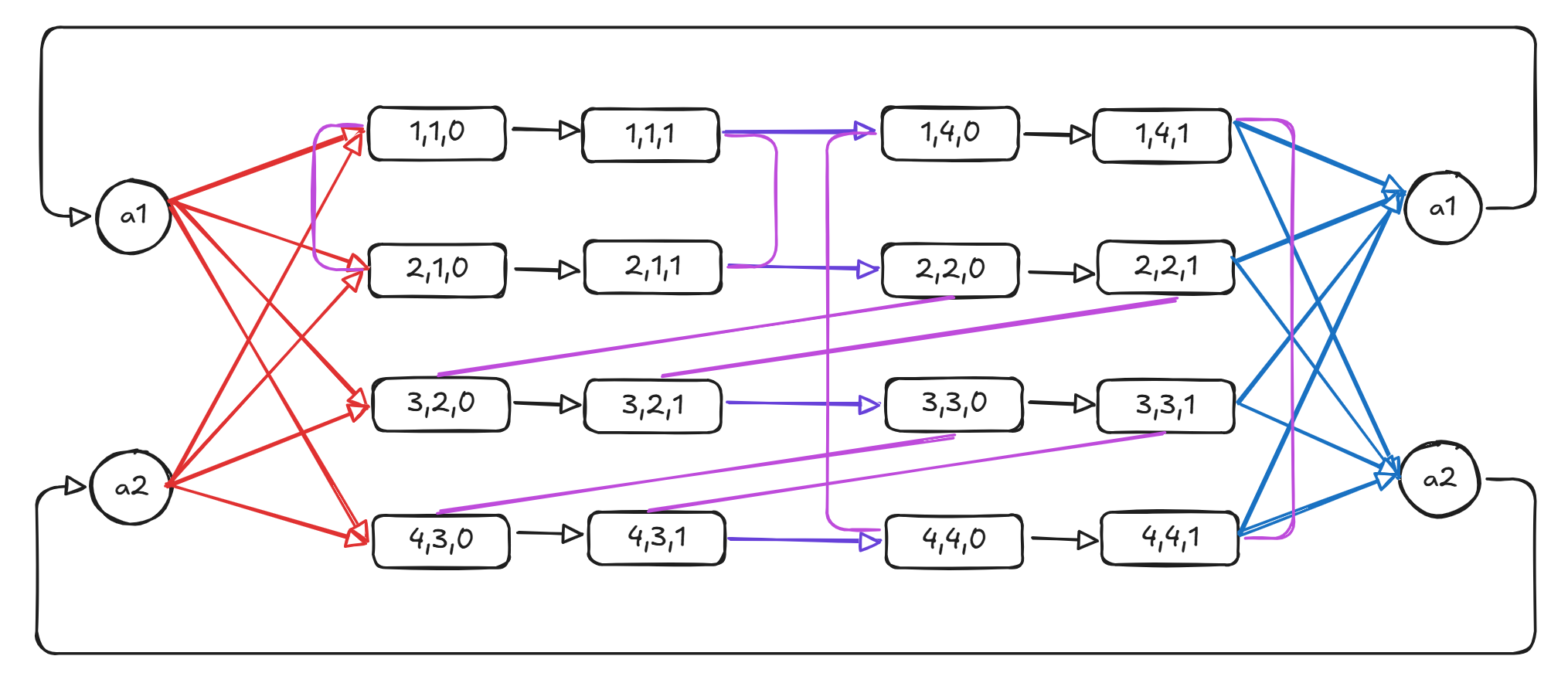
    alt text

    其中每种颜色对应了一种边, 没有箭头的边是双向边;

    同时图中有两个 , 表示的是同一个点 (只是为了方便连线, 左右各复制了一组 )

    可以看出, 每次从左到右依次遍历点, 当走到 , 可以从最右边跳回最左边, 算作选择了一个点;

    如果在选择完 时 或 之前, 将整个图所有点遍历了一遍, 说明在原图 中将所有边都覆盖了, 所以新图的一个 hamilton 环对应了原图的一个 node cover

    图中一条路径为



    表示选择了 两个点

    走黑色边代表覆盖了第 条边

    走浅紫色边代表覆盖正反第 条边

    走紫色边代表从与 相连的第 条边走到第 条边. 这个过程覆盖了与 相连的所有边

    走蓝色, 红色边代表用 选择某个点作为 node cover 的解

  8. directed hamilton circuit undirected hamilton circuit

    alt text

    直接将原图复制成 份, 相同编号点之间连线, 号点向 号点按照原图边集连边

    • 为什么复制 份? 感觉复制 份也可以?

  9. SAT 3-SAT

    alt text

    就是可以把所有 的子句递归地拆成 的子句

    1. 3-SAT chromatic number

    alt text

    这个画图都说不清楚了, 边太极八多了

    注意所有子句组成的点集

    假设

    这是一个不可满足的例子

    首先 与 不同色

    然后 两两相连, 所以他们颜色各不相同, 相当于创建了 种颜色

    不妨设

    接下来 和 保证了 , 即对应第 种字符的颜色就是

    然后 和 保证了

    alt text

    可以看到, 此时 使得 只有 种颜色可用, 但是这些边又要求 颜色互不相同

    所以不可满足

  1. chromatic number clique cover

    alt text

    如果 clique cover 中有 个团, 那么所有满足 的边都在 clique cover 的图中

    所以反图所有的边满足

    1. chromatic number exact cover

    exact cover 相当于 set packing 和 set covering 的结合版

    alt text

  1. exact cover hitting set

    alt text

    exact cover 中的每个集合 对应着 hitting set 中的每个元素 ; exact cover 中的每个元素 对应着 hitting set 中的每个集合

    如果 hitting set 中 , 说明 exact cover 中对应的 没有被覆盖, 不满足

    如果 hitting set 中 , 说明 exact cover 中对应的 被覆盖了两次及以上, 不满足 互不相交

    例如, exact cover 中

    那么对应的 hitting set 中

    并且 exact cover 中选出的 的下标对应着 hitting set 中 的元素

    例如

    所以对应的

  2. exact cover steiner tree

    alt text

    , 即需要覆盖所有的元素 和根节点

    从根 向所有 连边, 每条边权为

    之后将所有满足 的两点间连边, 边权为

    这样如果能够覆盖所有的 并且没有重复覆盖, 那么边权一定等于

  3. exact cover 3D matching

    3D matching 是说集合 中的每个点两两之间不能有任一维坐标相同, 即这些点每一维的坐标都恰好组成

    alt text

    alt text

    这泰庙辣

    是任意的 映射

    接下来对于 , 要求对于所有集合 对应的边 , 这个映射要将所有边转一遍, 从而构成一个局部的环

    对于映射 , 我们把所有 拿出来, 这些边正好把 覆盖掉, 此时只有这些边正好组成了对应的 的所有边, 才能保证所有 互不相交

    同时, 在这个假设下, 中的 项的第一维应该恰好对应集合 中的所有边

    那么如果这些边 的 都不属于 中的某个下标, 那么 项的第二维选择 , 应该正好在第二, 三维将这些边覆盖掉, 并且两两之间不同

    这是因为这些边构成了一些置换环, 那么长度为 的环刚好覆盖了某个 的所有边

    例如, 用 中的例子:

    那么不妨假设 , 即 是下标最小的包含 的集合

    那么有

    此时有

    项 项

    这里的 决定了我们选择了打对勾的 个点, 加上 的 个点构成了 3D matching 的

    可以发现 这些点中的 的 刚好为 , 对应着我们在 exact cover 中选择的

    对应的图为

    alt text

    其中红色便对应着 选择的边, 蓝色表示 中的边

    如果将 改成 , 此时的 就不存在 exact cover 了

    而此时的表变成

    𝟚𝟚
    𝟛𝟚
    项 项
    𝟚𝟙𝟚𝟚𝟚𝟚 𝟚𝟚

    此时无论选取 还是 , 都会和 项中的坐标重复

    并且除了这一种 的选取方式, 其他任意一种 都不行

    所以原问题不存在 exact cover

  4. exact cover knapsack

    alt text

    令 , 可以构造出一个 的常数

    然后

    这里的 相互正交 ( 进制表达), 恰好可以对应原问题的

    用 表示是否选择 , 即在原问题中是否选择了

    所以如果有 , 并且

  5. knapsack sequencing

    alt text

    按照图中方法转换, 无论 取值, 求出来的解一定对应了原问题的一个解, 使得某一个下标 之前的时间序列满足

    所以对应着原问题的解

    • 对于这个不等号, 和 中一样, 我们可否改变背包问题的定义为 ?

      (因为我们一般要求能装下就行, 不要求一定要刚好等于容量)

  6. knapsack partition

    alt text

    如果存在一个分割 , 使得 与 不在同一组, 并且两组和相等

    那么

    移项得到

    所以 就是背包的下标解集

    如果 与 在一组, 那么

    移项得到 , 不满足 , 舍弃

    • 如果想要反着归约 partition knapsack, 该怎么做?

      可以尝试将原式同加一个 , 变成

      所以令 即可

  7. partition max cut

    alt text

    如果满足 , 则有

    即

    这等同于

    所以

    所以一定满足 , 即

    所以 是原问题的一个分割

参考 :

Cook 原论文

Karp 原论文