transformer

结构

Encoder/Decoder

单个 encoder/decoder 结构:

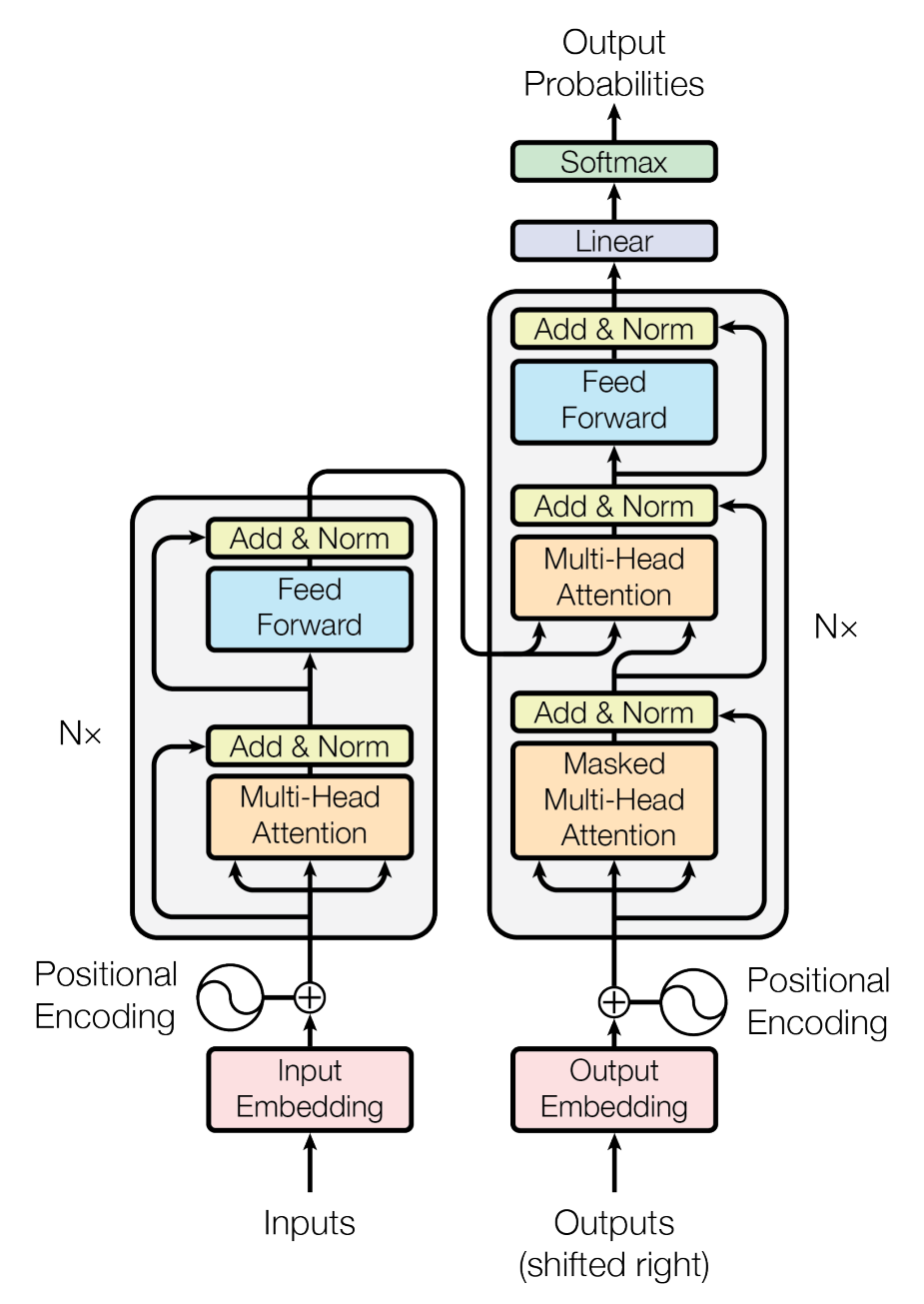
一共有 层这样相同的结构, 组成整个 transformer

左边是 encoder, 右边是 decoder

1. encoder 有两个子层, 每层的输出为 , 其中 为输入, 是这一子层的函数

   输出的维数

2. decoder 有三个子层, 中间一层将 encoder 的输出作为多头注意力的 输入, 将上一子层的输出作为 输入

   同时第一层加入了掩码, 使位置 的预测只依赖于 之前的输出, 而不会注意到后面的输出

最后的 linear 层可以把 decoder 输出转换成整个单词表的矩阵

经过 softmax 后得到每个单词的概率

事实上 linear 层是 embedding 层的转置, 他们共享参数

假设 embedding 层的系数矩阵为

做 embedding 时, 将从第 层选择一行向量作为 embedding

在 linear 层的输入会与 linear 层的系数矩阵 相乘得到一个

的矩阵

其中 是序列长度

由于 linear 层的输入是学习过的 decoder 输出, 所以通过学习 decoder 内系数, 得到的 的矩阵每一行代表着单词出现的分数

经过 softmax 变成出现概率

Attention

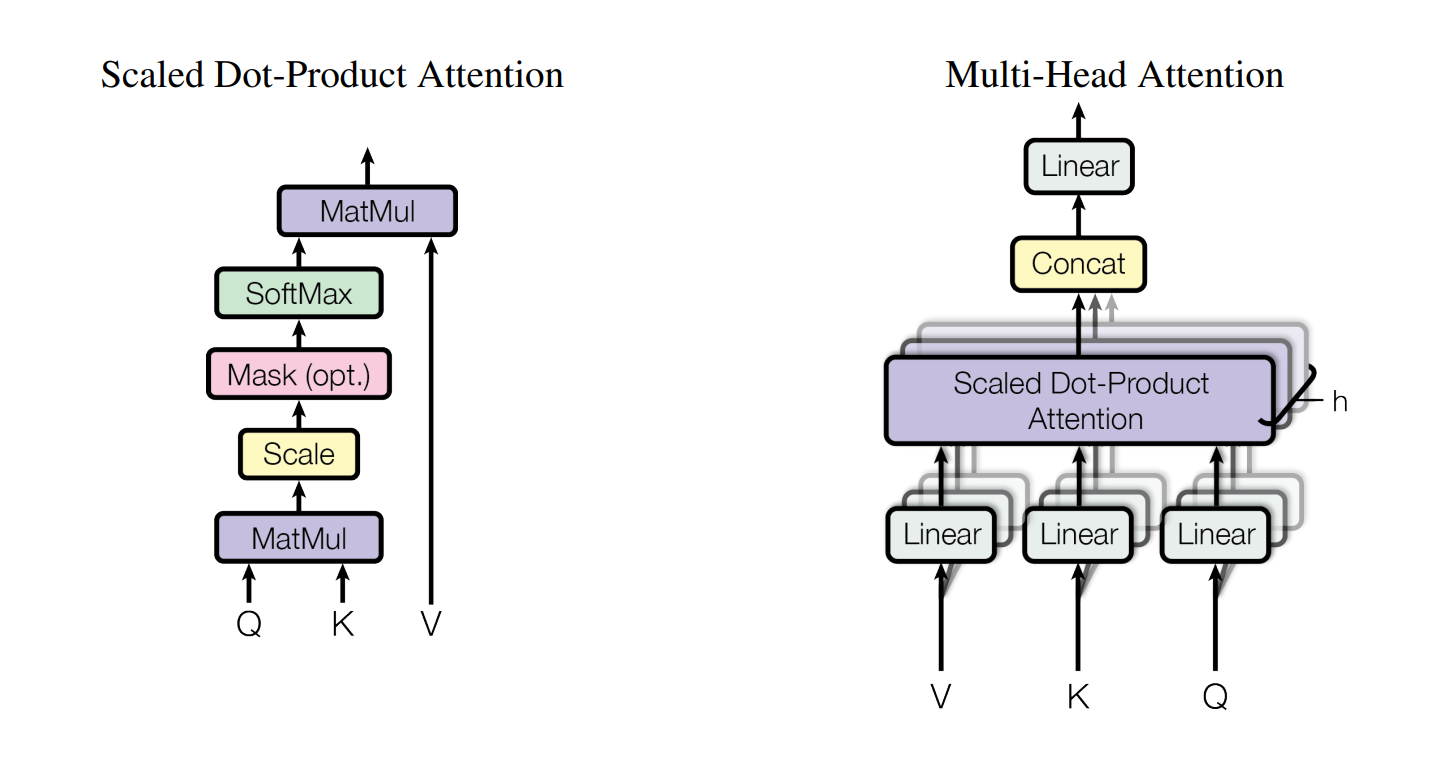
三个输入

是查询 (queries), 时键值对 (keys and values)

1. Scaled Dot-Product Attention

   假设 维数为 , 维数为

   输出表示为

   • 对于注意力的选择

     有两种主流注意力: Additive 和 Dot-Product

     一般来说, 点积可以矩阵优化, 所以比加法的快

     但是当 很大时, 点积会造成梯度趋近于 , 导致效果变差

     乘上 规范化系数可以避免这个问题

   • 注意力的 意义? 与所有 计算相似度 (点积), 得出的是对应 的权重; 之后将 加权求和输出

     所以 是输入信息, 也就是查询, 是输入信息与对应的输出组成的键值对, 是位置表示以及对应的答案

     一般来自于相同的输入

     在自注意力中, 也来自于相同输入, 这样可以注意到句子中各个单词的依赖关系

   • 复杂度: ,

     其中序列长度为 , 向量维数为

     那么 复杂度为

     复杂度为

     所以复杂度为

   • 如果改成 restricted, 每个元素只能和周围 个元素计算依赖, 即

     所以复杂度为

2. Multi-Head Attention

   先把 线性映射成不同的 组 维向量

   然后并列 个 Scaled Dot-Product Attention

   输出表示为

   其中 都是系数矩阵, 上标不是乘方, 只是表示方法

   一般取

   • 为什么设计成多头注意力? 一方面是为了从不同角度/子空间思考, 注意到不同语义和句法; 同时可以并行计算

   • 复杂度: 这里的 , 因为是其他层的输出

     计算是

     并且

     最终计算 的复杂度是

     所以复杂度为

   • 如果改成 restricted, 那么

     计算复杂度为

     计算复杂度为

     所以总的复杂度是

3. Transformer 中的 Attention

   • 在 decoder 的第二层使用 cross attention, 将上一层 decoder 输出作为 query, 将 encoder 输出作为 key, value

     这样能够让 decoder 的每个位置都注意到 encoder 的所有位置

   • 在 encoder 的第一层使用 self attention, 让 encoder 的每个位置注意到 encoder 自己的所有位置

   • 在 decoder 的第一层使用 self attention, 让 decoder 的每个位置注意到 encoder 对应的在自己之前的位置

     为了达到自回归的目的

     可以在点积自注意力的 softmax 前加一个 mask 层

     具体为一个三角矩阵, 形如:

     由于行代表 decoder, 列代表 encoder, 所以这个矩阵可以让 decoder 只注意到自己位置之前的 encoder 输入

     这个矩阵与原本的计算结果相加后 softmax, 会让上三角变成全 , 达到消除单词与后面单词依赖性的目的

Position-wise Feed-Forward Networks

全连接层, 函数是两个线性变换加上一层 ReLU:

层与层之间的参数各不相同

• 这样的变换有什么意义?

  中间的 ReLU 引入了非线性成分, 可以更好地拟合任意函数

  具体见 博客

Embeddings and Softmax

embedding 将单词转换成维数为 的向量, 一般是 MLP

Positional Encoding

transformer 结构中没有 RNN, CNN

为了加入一些单词之间的位置信息, 加入了两个函数:

是位置, 是维数

这样输入的每一维对应着一个三角函数

由于三角函数的性质, 对于任意 , 都可以将 表示成 的线性函数

• 线性性的好处具体体现? 这可能使学习相对位置信息更简单; 同时它允许接受比训练时的最大句子长度更长的输入句子

对比 RNN, CNN

Layer Type	Complexity per Layer	Sequential Operations	Maximum Path Length
Self-Attention
Recurrent
Convolutional
Self-Attention(restricted)

序列长度为 , 向量维数为 , CNN 的卷积核大小为 , 限制自注意力的块大小为

---

并行计算

复杂度是

主要关注三点:

复杂度

每层计算的复杂度

1. 对于 RNN, 可以用最经典的计算公式 来看复杂度

   是 时刻输入, 维数是

   是上一个隐藏层, 维数是

   是参数矩阵, 维数是

   所以单次迭代复杂度是 , 这一层处理整个序列复杂度

2. 对于 CNN, 输入/输出通道维数都是

   那么 个单词组成了 的输入数据

   一个卷积核维数是 , 是卷积核的宽度, 也是时间步, 意义是跨越 个单词, 从而学习单词间的局部依赖

   所以单次计算卷积的复杂度是

   而计算出的值是一个实数, 对应着某个输出通道的值

   要想计算所有输出通道的值, 就需要 个这样的卷积核, 计算复杂度是

   所以实际整个卷积核的维数是 的

   那么计算整个序列, 复杂度是

3. 对于 transformer, 如果只考虑 Self-Attention 的计算部分, 那么复杂度是 的 (即忽略了线性映射的 )

   • 为什么可以忽略线性映射部分?

• 相当于并行计算的 , 即每一组的 workload

可并行计算的工作量

哪个层结构的序列操作数量最少

长距离依赖的学习效率

哪个层结构的最大路径长度最少

最大路径是指前向/后向传播途径的路径

网络中的路径长度决定了词与词之间长距离依赖的学习效率

所以最大路径长度越短, 学习依赖越简单 (效率越高)

• 相当于并行计算的 , 即 depth

综合对比一下

1. 对于计算的复杂度, RNN 的 要优于普通 CNN 的 , 是卷积核 (kernel) 的大小,

   同时, 在 时普通的自注意力优于 RNN

   为了提升长序列的表现, 可以将输入序列分组, 每组长为 , 分成 组. 这样的限制自注意力比 RNN 的序列操作更少; 尽管这会提升最大路径长度, 但仍然好于 RNN 的最大路径长度

   如果 , 那么这样的自注意力就会好于 RNN

2. 对于 Separable convolutions, 复杂度达到了 , 但仍然不比 的限制自注意力的 好

   • 对于最大路径长度, 如何比较 与 , 或者比较 与 ?

3. 上面说了 restricted Self-Attention 还有一个 的线性映射部分, 同时 也为 ; 不过就算加上这两部分, 复杂度是 , 在 时, 这个复杂度与 RNN 的 和 CNN 的 基本等价

   并且注意力可以更好地学习到长程依赖, 还比 RNN 具有更好的可并行性

4. 还有一个 interpretability 的好处, 不太懂

   大概是说可以理解更多语义和句法

   原文 有更详细描述

---

• Attention 的灵感来自于哪里? 背后的数学/物理模型好像和自旋系统/能量什么的有关?
• readme

---

参考: Attention Is All You Need