Pairing Heap

(Updated: )

Pairing Heap

Operations

Find-Min

直接返回根节点

Meld

合并两个堆

把两个堆中权值小的根节点 作为根节点，把另一个根节点 作为儿子插入到这个节点

由于配对堆需要维护一个精巧的顺序，所以对一个节点，左边的儿子是最新加入的，右边是最早加入的

所以 插入到当前根节点 的儿子，把之前的儿子设为 兄弟即可

1
2
3
4
5
6
7
8
9
10
template<typename T> Node<T>* meld(Node<T>* x, Node<T>* y){
    if(!x) return y;
    if(!y) return x;
    if(x->value > y->value) swap(x, y);
    y->sibling = x->child;
    if(x->child) x->child->father = y;
    x->child = y;
    y->father = x;
    return x;
}

insert

将新节点与原有堆合并

Merge

这个函数将节点 及其右边的兄弟合并成一个堆

我们希望先将两个堆两两配对合并成一个新的堆，再从右到左合并这些堆

递归地说，就是将当前两个堆合并，然后递归两个堆右边的所有堆，最后将合并的堆与递归的堆合并

1
2
3
4
5
6
7
8
9
10
Node<T>* merge(Node<T>* x){
    if(!x) return x;
    x->father = NULL;
    if(!x->sibling) return x;
    Node<T>* y = x->sibling;
    Node<T>* c = y->sibling;
    y->father = NULL;
    y->sibling = x->sibling = NULL;
    return meld(merge(c), meld(x, y));
}

Delete-Min

将根节点删除，并将根的儿子进行 merge, 将得到的返回指针作为新的根

Decrease-Key

将节点 权值减小

由于权值减小不影响 的儿子与它的顺序，所以不用改 的儿子

只需要将 从它那一层抽出来，维护原有对结构，并将 与原有的堆合并即可

1
2
3
4
5
6
7
8
9
10
11

Node<T>* decrease_key(Node<T>* x, T value){
    x->value = value;
    if(x == root) return x;
    if(x->father->child == x) x->father->child = x->sibling;
    else x->father->sibling = x->sibling;
    if(x->sibling) x->sibling->father = x->father;
    x->sibling = x->father = NULL;
    // because value decreases, so x->child doesn't need to be modified
    return meld(root, x);
}

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include<bits/stdc++.h>
using namespace std;
template<typename T> 
class Pairing_Heap;
template<typename T> 
class Node{
public:
    T value;
    Node<T>* child;
    Node<T>* sibling;
    Node<T>* father;
    Node<T>(){}
    Node<T>(T value) : value(value){child = NULL, sibling = NULL, father = NULL;}
    friend class Pairing_Heap<T>;
};

template<typename T> 
class Pairing_Heap{
public:
    Node<T>* root;
    Pairing_Heap<T>(){root = NULL;}
    Node<T>* meld(Node<T>* x, Node<T>* y){
        if(!x) return y;
        if(!y) return x;
        if(x->value > y->value) swap(x, y);
        y->sibling = x->child;
        if(x->child) x->child->father = y;
        x->child = y;
        y->father = x;
        return x;
    }
    Node<T>* merge(Node<T>* x){
        if(!x) return x;
        x->father = NULL;
        if(!x->sibling) return x;
        Node<T>* y = x->sibling;
        Node<T>* c = y->sibling;
        y->father = NULL;
        y->sibling = x->sibling = NULL;
        return meld(merge(c), meld(x, y));
    }
    void insert(T value){
        Node<T>* NewNode = new Node<T>(value);
        root = meld(NewNode, root);    
    }
    T find_min(){
        return root->value;
    }
    Node<T>* erase_min(Node<T>* x){
        Node<T>* t = merge(x->child);
        delete x;
        return t;
    }
    T delete_min(){
        T ret = root->value;
        root = erase_min(root);
        return ret;
    }
    Node<T>* decrease_key(Node<T>* x, T value){
        x->value = value;
        if(x == root) return x;
        if(x->father->child == x) x->father->child = x->sibling;
        else x->father->sibling = x->sibling;
        if(x->sibling) x->sibling->father = x->father;
        x->sibling = x->father = NULL;
        // because value decreases, so x->child doesn't need to be modified
        return meld(root, x);
    }
};

复杂度证明

势能函数

与 Splay 的势能函数相同

其实这个堆 Tarjan 也参与了研究

你真是万恶之源

定义每个节点子树大小为

势能函数为

操作

对于 make_heap, find_min, 势能不变，所以都是均摊

操作

对于 insert, meld, decrease_key, 将一个堆连接到另一个堆根的儿子上，势能变化最大为

并且这些操作实际代价都是

所以这些操作都是均摊

delete_min 操作

实际代价

对于 delete_min, 把根删除势能减少为

另外把配对和配对后的所有堆顺序合并分开讨论

由于配对过程的连接操作至少与顺序合并过程的连接一样多

所以连接实际代价最大为 倍配对连接代价

设一共 对配对，所以代价最大为

另外除了连接的操作为

所以实际代价最大为

这里直接 , 因为势能函数里 足够大，所以实际代价和下面的势能变化都简化表示了

配对

对于配对，形式类似于下图:

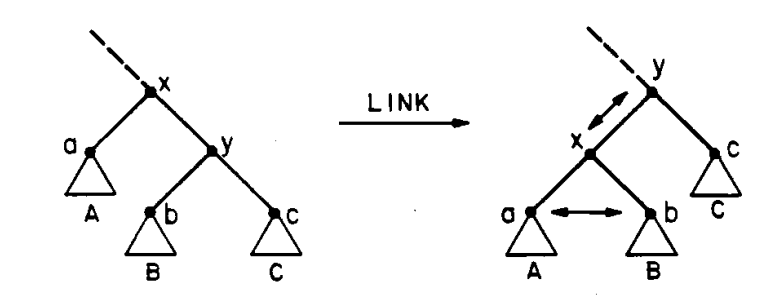
alt text

假设 初始非空，势能变化为

同时由于 , 当 时取到

所以我们有:

同时因为

所以结合上式有

同时唯一可以使 为空的连接操作只有最后一个

势能变化最大为

将前 次势能变化 求和，再加上最后一次 得到:

由于

顺序合并

对于顺序合并, 形式类似于下图:

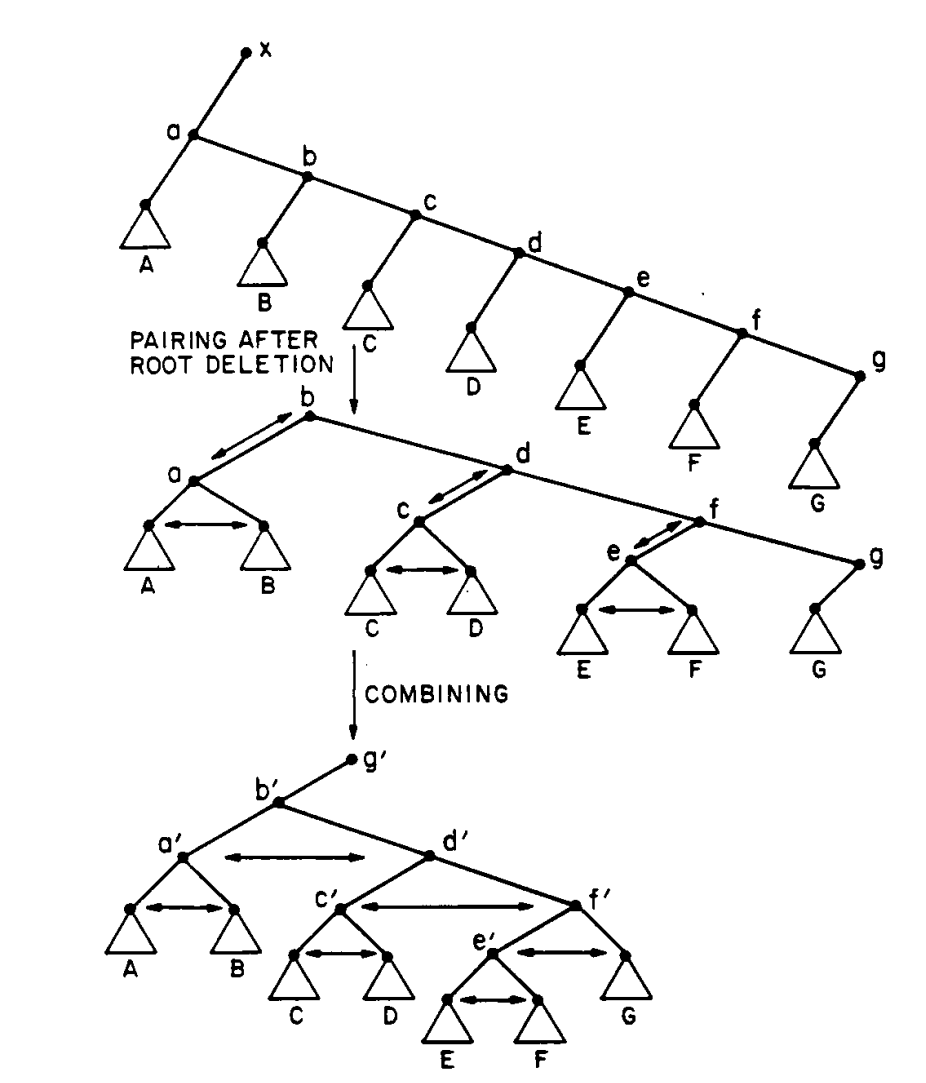
alt text

在讨论节点势能变化时，我们可以构造一个双射 使得对于除了合并后的根的所有点, 都有 , 表示合并后的节点子树大小

对于图中, 除了 , 其他节点都可以找到原图中比它子树大小大的节点

这是因为，一次合并的结果有两种，结构变和不变

结构变化后与树做了一次旋转是一样的:

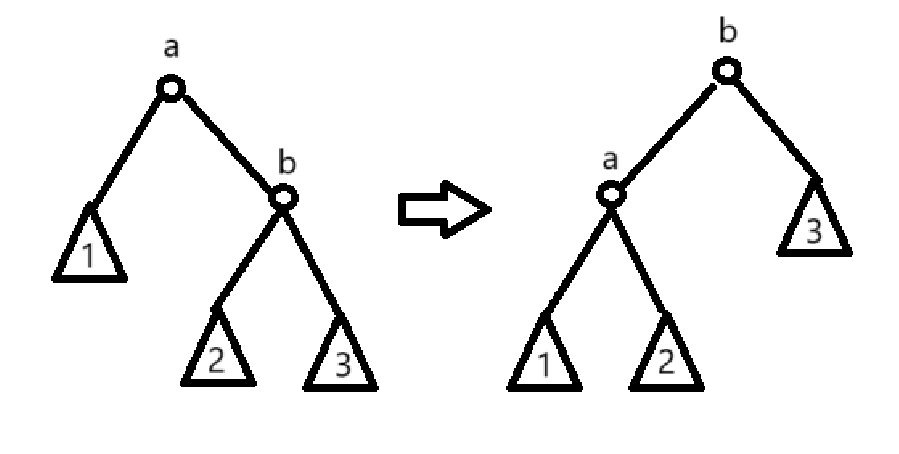
alt text

对于 子树势能不变

对于新的 , 它的大小不比原本的 大

所以只有新的根 增大

对于合并后的根, 势能最大为

其余节点在映射后势能不增

所以势能增大最大为

所以总的均摊代价为

所以 delete_min 均摊为

  • 参考: 原论文

  • 注: 原论文认为这个堆的各操作复杂度应该和 Fibonacci Heap 相同，只是他们只证明了除了 make_heap, find_min 以外的操作是 的

  • 但是目前有证明说明 decrease_key 下界至少为