Mersenne Twister

MT19937

算法

一个可以产生循环节长为 的随机数的算法

令 表示一个二进制 word 的长度; 加粗的 表示长为 的 向量. 也就是长度为 的二进制数

给出迭代式子:

其中:

是向量空间中向量的个数，初始的 随机选取

我们后面的迭代操作都是在 这个向量空间上迭代的

表示 的高 位, 表示 的低 位

其实 就是将 高低位拼接起来

矩阵具体长成：

这样的形式 的计算会比较快

因为我们有

其中 ,

同时，定义一个序列 是在 -分布下 位精确的, 如果将 个 的高 位组成一个 长度的向量，在序列的一个周期中，对于所有可能的 中组合，都出现了相等次数

为了提升 -分布下 位精确, 我们在得到 之后, 还要将其做一个变换

等价于使用位运算:

算法实际是在向量空间上的迭代，向量空间为一个数组：, 即最后一个向量缺失了最后 位

将这样的数组拼接起来，变成长为 的数组

那么迭代的过程用矩阵表示：

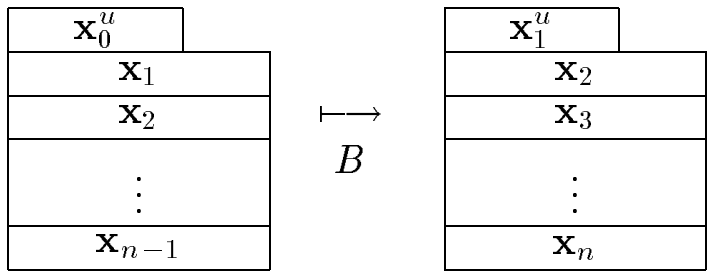
其中 的特征多项式为

对于这样一个使用 迭代的迭代式，有这样一个定理:

定理: 序列可以达到最大循环节 , 当且仅当特征多项式 是本原多项式

这里的本原多项式指所有系数互素的多项式

更具体地说, 它指的是不能分解成两个多项式乘积，并且可以基于一个域生成另一个拓展域的所有元素的多项式

对于 “不能分解成两个多项式乘积” 这个性质好理解，和质数相似

对于 “生成另一个拓展域的所有元素” 这个性质，可以参见伽罗华域中本原多项式的应用

定理的证明见原论文的 THEOREM 4.1

整个算法流程为:

在 算法中, 选取如下参数:

可以看到 , 这是算法名称的由来

同时, 这样的系数使得算法循环节为 , 同时具有很好的 -分布性质 (即分布很均匀).

代码

#include<bits/stdc++.h>
using namespace std;
template<typename T> class MT{
public:
    #define N 624
    #define M 397
    #define A 0x9908b0df
    #define UPPER 0x80000000
    #define LOWER 0x7fffffff
    #define B 0x9d2c5680
    #define C 0xefc60000
    #define U(y) (y >> 11)
    #define S(y) (y << 7)
    #define T(y) (y << 15)
    #define L(y) (y >> 18)
    T mt[N];
    int mti; // initially N + 1 means sgenrand() not called
    int seed;
    MT(){mti = N + 1;}
    MT(int seed) : seed(seed){mti = N + 1, sgenrand(seed);}
    void sgenrand(int seed){
        mt[0] = seed & 0xffffffff;
        for(mti = 1; mti < N; ++mti){
            mt[mti] = (69069 * mt[mti - 1]) & 0xffffffff;
        }
    }
    T operator () () {
        genrand();
    }
    T genrand(){
        T y;
        if(mti >= N){
            if(mti == N + 1) sgenrand(114514); 
            // seed not set, use default seed
            // you can also use 1919810 XD
            for(int i = 0; i < N; ++i){
                y = (mt[i] & UPPER) | (mt[(i + 1) % N] & LOWER);
                mt[i] = mt[(i + M) % N] ^ (y >> 1) ^ (y & 1 ? A : 0);
            }
            mti = 0;
        }
        y = mt[mti++];
        y ^= U(y), y ^= S(y), y ^= T(y), y ^= L(y);
        return y;
    }
}; 

void solve() {
    MT<unsigned long> rd(time(0));
    for(int i = 0; i < 10; ++i){
        cout << rd() << endl;
    }
}
int main() {
    solve();
    return 0;
}

安全性

由于所有操作都可以用位运算完成，所以不难逆向

除非将得到的随机数使用 映射掉，否则这个算法并不算安全

---

• 参考: MT原论文