Geometrical Optics

光学的费马定理

叙述

这说明了：

, 则时间只能取极值或为常值

语言描述就是：光走的路径是用时最短的路径

这也说明时间取的是极小值

下面给出一些数学定义

数学

泛函

泛函是从函数组成的向量空间到标量域的映射

线性代数里的线性泛函就是从向量空间映射到数域

一般的泛函将函数映射到实数域

例如对于函数做定积分，得到一个实数值，那么这个积分就是对于函数的泛函

也就是说，函数是把值映射到值，泛函是把函数映射到值

变分

微分是变量的变化量，比如自变量从 变化到 , 变化量为

而变分是指函数的变化量，比如自变量函数从 变化到 , 变化量为 ， 也可写成

变量的变化量是一个值，函数的变化量是一个函数。所以感性理解一下，微分是针对函数的，变分是针对泛函的

更具体/严格定义变分，应该长成类似这样：

如果函数从 变化到 , 那么 , 其中 是一个变量

具体见 wiki

Euler-Lagrange 方程

一般的方程为:

如果 , 并且 , 即 不显含

则方程写成:

是函数 的一个泛函

我们想要找到一个函数 使得 取极值

也就是找到 使得

事实上，这样的 满足 Euler-Lagrange 方程:

这是由于

并且

所以变分与微分可交换次序

将第二部分分部积分

由于边界是固定的, 所以 , 所以第一部分为 , 只剩第二部分

所以

因为 是任意的，所以要对于任意 都有 , 就得出

例子

同时，在 不显含 时，有等价的式子:

若 , 则 等价于

应用到费马定理

费马定理中，

一般是分段常值函数

, 所以代入上面的式子

即:

若路径与铅垂线夹角为 , 那么

首先，对于反射定律:

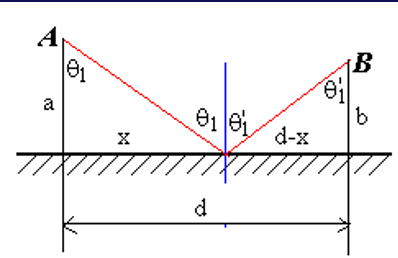
由于 不变，所以 不变，所以

其次，对于折射定律:

, 即如果 是位置的连续函数，则 是一个常数

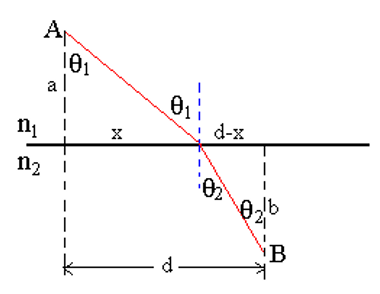
这可以得到折射定律:

此外还可以得到大气中光线轨迹的微分方程：

• 图源：Minghu Fang PPT